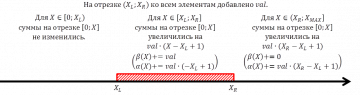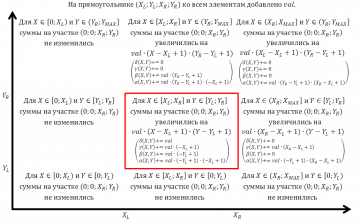Варианты дерева Фенвика: различия между версиями
Перейти к навигации
Перейти к поиску
Ctrlalt (обсуждение | вклад) |
Ctrlalt (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
== Одномерное дерево Фенвика == | == Одномерное дерево Фенвика == | ||
int | int f[MAX_SIZE]; | ||
int | int query(int r) { | ||
int res = 0; | int res = 0; | ||
for (int i = | for (int i = r; i >= 0; i = (i & (i + 1)) - 1) | ||
res += | res += f[i]; | ||
return res; | return res; | ||
} | } | ||
void | void modify(int r, int val) { | ||
for (int i = | for (int i = r; i < MAX_SIZE; i |= i + 1) | ||
f[i] += val; | |||
} | } | ||
=== Запрос суммы на отрезке, изменение отдельных элементов === | === Запрос суммы на отрезке, изменение отдельных элементов === | ||
query(r) — сумма элементов от 0-го до r-го. | |||
int | int prefixSum(int r) { | ||
return | return query(r); | ||
} | } | ||
void add(int | void add(int pos, int val) { | ||
modify(pos, val); | |||
} | } | ||
=== Запрос значений отдельных элементов, изменение на отрезке === | === Запрос значений отдельных элементов, изменение на отрезке === | ||
query(r) — значение r-го элемента. | |||
int get(int | int get(int pos) { | ||
return | return query(pos); | ||
} | } | ||
void add(int l, int r, int val) { | void add(int l, int r, int val) { | ||
modify(l, val); | |||
modify(r + 1, -val); | |||
} | } | ||
=== Запрос суммы на отрезке, изменение на отрезке === | === Запрос суммы на отрезке, изменение на отрезке === | ||
Tx.query(r) * r + T.query(r) — сумма элементов от 0-го до r-го. | |||
[[Файл:fenwick_range_1d.png|thumb|right|360px]] | [[Файл:fenwick_range_1d.png|thumb|right|360px]] | ||
int | int prefixSum(int r) { | ||
return | return Tx.query(r) * r + T.query(r); | ||
} | } | ||
void add(int l, int r, int val) { | void add(int l, int r, int val) { | ||
Tx.modify(l, val); | |||
Tx.modify(r + 1, -val); | |||
T.modify(l, val * (-l + 1)); | |||
T.modify(r + 1, val * r); | |||
} | } | ||
== Двумерное дерево Фенвика == | == Двумерное дерево Фенвика == | ||
int | int f[MAX_SIZE][MAX_SIZE]; | ||
int | int query(int ry, int rx) { | ||
int res = 0; | int res = 0; | ||
for (int i = | for (int i = ry; i >= 0; i = (i & (i + 1)) - 1) | ||
for (int j = | for (int j = rx; j >= 0; j = (j & (j + 1)) - 1) | ||
res += | res += f[ry][rx]; | ||
return res; | return res; | ||
} | } | ||
void | void modify(int ry, int rx, int val) { | ||
for (int i = | for (int i = ry; i < MAX_SIZE; i |= i + 1) | ||
for (int j = | for (int j = rx; j < MAX_SIZE; j |= j + 1) | ||
f[i][j] += val; | |||
} | } | ||
=== Запрос суммы на прямоугольнике, изменение отдельных элементов === | === Запрос суммы на прямоугольнике, изменение отдельных элементов === | ||
query(ry, rx) — сумма элементов от (0; 0)-го до (ry; rx)-го. | |||
int | int prefixSum(int ry, int rx) { | ||
return | return query(ry, rx); | ||
} | } | ||
void add(int | void add(int ry, int rx, int val) { | ||
modify(ry, rx, val); | |||
} | } | ||
=== Запрос значений отдельных элементов, изменение на прямоугольнике === | === Запрос значений отдельных элементов, изменение на прямоугольнике === | ||
query(ry, rx) — значение (ry; rx)-го элемента. | |||
int get(int | int get(int ry, int rx) { | ||
return | return query(ry, rx); | ||
} | } | ||
void add(int | void add(int ly, int lx, int ry, int rx, int val) { | ||
modify(ly, lx, val); | |||
modify(ry + 1, lx, -val); | |||
modify(ly, rx + 1, -val); | |||
modify(ry + 1, rx + 1, val); | |||
} | } | ||
=== Запрос суммы на прямоугольнике, изменение на прямоугольнике === | === Запрос суммы на прямоугольнике, изменение на прямоугольнике === | ||
Tyx.query(ry, rx) * x * y + Ty.query(ry, rx) * y + Tx.query(ry, rx) * x + T.query(ry, rx) — сумма элементов от (0; 0)-го до (ry; rx)-го. | |||
[[Файл:fenwick_range_2d.png|thumb|right|360px]] | [[Файл:fenwick_range_2d.png|thumb|right|360px]] | ||
int | int prefixSum(int ry, int rx) { | ||
return | return Tyx.query(ry, rx) * x * y + Ty.query(ry, rx) * y + Tx.query(ry, rx) * x + T.query(ry, rx); | ||
} | } | ||
void add(int | void add(int ly, int lx, int ry, int rx, int val) { | ||
Tyx.modify(ly, lx, val); | |||
Tyx.modify(ry + 1, lx, -val); | |||
Tyx.modify(ly, rx + 1, -val); | |||
Tyx.modify(ry + 1, rx + 1, val); | |||
Ty.modify(ly, lx, val * (-lx + 1)); | |||
Ty.modify(ry + 1, lx, -val * (-lx + 1)); | |||
Ty.modify(ly, rx + 1, val * rx); | |||
Ty.modify(ry + 1, rx + 1, -val * rx); | |||
Tx.modify(ly, lx, val * (-ly + 1)); | |||
Tx.modify(ry + 1, lx, val * ry); | |||
Tx.modify(ly, rx + 1, -val * (-ly + 1)); | |||
Tx.modify(ry + 1, rx + 1, -val * ry); | |||
T.modify(ly, lx, val * (-lx + 1) * (-ly + 1)); | |||
T.modify(ry + 1, lx val * (-lx + 1) * ry); | |||
T.modify(ly, rx + 1, val * rx * (-ly + 1)); | |||
T.modify(ry + 1, rx + 1, val * rx * ry); | |||
} | } | ||
== Ссылки == | == Ссылки == | ||
* [[Дерево Фенвика]] | * [[Дерево Фенвика]] | ||
* [http://arxiv.org/pdf/1311.6093v4.pdf Mishra P. A New Algorithm for Updating and Querying Sub-arrays of Multidimensional Arrays] | * [http://arxiv.org/pdf/1311.6093v4.pdf Mishra P. A New Algorithm for Updating and Querying Sub-arrays of Multidimensional Arrays] | ||
[[Category:Структуры данных для задач RSQ/RMQ]] | [[Category:Структуры данных для задач RSQ/RMQ]] | ||
Версия от 23:34, 22 июня 2016
Одномерное дерево Фенвика
int f[MAX_SIZE];
int query(int r) {
int res = 0;
for (int i = r; i >= 0; i = (i & (i + 1)) - 1)
res += f[i];
return res;
}
void modify(int r, int val) {
for (int i = r; i < MAX_SIZE; i |= i + 1)
f[i] += val;
}
Запрос суммы на отрезке, изменение отдельных элементов
query(r) — сумма элементов от 0-го до r-го.
int prefixSum(int r) {
return query(r);
}
void add(int pos, int val) {
modify(pos, val);
}
Запрос значений отдельных элементов, изменение на отрезке
query(r) — значение r-го элемента.
int get(int pos) {
return query(pos);
}
void add(int l, int r, int val) {
modify(l, val);
modify(r + 1, -val);
}
Запрос суммы на отрезке, изменение на отрезке
Tx.query(r) * r + T.query(r) — сумма элементов от 0-го до r-го.
int prefixSum(int r) {
return Tx.query(r) * r + T.query(r);
}
void add(int l, int r, int val) {
Tx.modify(l, val);
Tx.modify(r + 1, -val);
T.modify(l, val * (-l + 1));
T.modify(r + 1, val * r);
}
Двумерное дерево Фенвика
int f[MAX_SIZE][MAX_SIZE];
int query(int ry, int rx) {
int res = 0;
for (int i = ry; i >= 0; i = (i & (i + 1)) - 1)
for (int j = rx; j >= 0; j = (j & (j + 1)) - 1)
res += f[ry][rx];
return res;
}
void modify(int ry, int rx, int val) {
for (int i = ry; i < MAX_SIZE; i |= i + 1)
for (int j = rx; j < MAX_SIZE; j |= j + 1)
f[i][j] += val;
}
Запрос суммы на прямоугольнике, изменение отдельных элементов
query(ry, rx) — сумма элементов от (0; 0)-го до (ry; rx)-го.
int prefixSum(int ry, int rx) {
return query(ry, rx);
}
void add(int ry, int rx, int val) {
modify(ry, rx, val);
}
Запрос значений отдельных элементов, изменение на прямоугольнике
query(ry, rx) — значение (ry; rx)-го элемента.
int get(int ry, int rx) {
return query(ry, rx);
}
void add(int ly, int lx, int ry, int rx, int val) {
modify(ly, lx, val);
modify(ry + 1, lx, -val);
modify(ly, rx + 1, -val);
modify(ry + 1, rx + 1, val);
}
Запрос суммы на прямоугольнике, изменение на прямоугольнике
Tyx.query(ry, rx) * x * y + Ty.query(ry, rx) * y + Tx.query(ry, rx) * x + T.query(ry, rx) — сумма элементов от (0; 0)-го до (ry; rx)-го.
int prefixSum(int ry, int rx) {
return Tyx.query(ry, rx) * x * y + Ty.query(ry, rx) * y + Tx.query(ry, rx) * x + T.query(ry, rx);
}
void add(int ly, int lx, int ry, int rx, int val) {
Tyx.modify(ly, lx, val);
Tyx.modify(ry + 1, lx, -val);
Tyx.modify(ly, rx + 1, -val);
Tyx.modify(ry + 1, rx + 1, val);
Ty.modify(ly, lx, val * (-lx + 1));
Ty.modify(ry + 1, lx, -val * (-lx + 1));
Ty.modify(ly, rx + 1, val * rx);
Ty.modify(ry + 1, rx + 1, -val * rx);
Tx.modify(ly, lx, val * (-ly + 1));
Tx.modify(ry + 1, lx, val * ry);
Tx.modify(ly, rx + 1, -val * (-ly + 1));
Tx.modify(ry + 1, rx + 1, -val * ry);
T.modify(ly, lx, val * (-lx + 1) * (-ly + 1));
T.modify(ry + 1, lx val * (-lx + 1) * ry);
T.modify(ly, rx + 1, val * rx * (-ly + 1));
T.modify(ry + 1, rx + 1, val * rx * ry);
}