Множество и словарь. Реализация на деревьях поиска: различия между версиями
Ctrlalt (обсуждение | вклад) |
Ctrlalt (обсуждение | вклад) Нет описания правки |
||
| (не показаны 72 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
< | == TLDR == | ||
<youtube width="300" height="180">8Gdp7XJeW5g</youtube> | |||
== Общие сведения == | == Общие сведения == | ||
| Строка 18: | Строка 19: | ||
Операции словаря похожи на операции множества, но в качестве параметров принимают ключи, а не непосредственные значения элементов. | Операции словаря похожи на операции множества, но в качестве параметров принимают ключи, а не непосредственные значения элементов. | ||
{| | {| class="methodlist" | ||
| | | || void || insert(T1 key, T2 value) || — добавление пары <tt>(key, value)</tt> в словарь; | ||
|- | |- | ||
| | | || void || remove(T1 key) || — исключение из словаря значения, сопоставленного с ключом <tt>key</tt>; | ||
|- | |- | ||
| | | || T2 || find(T1 key) || — получение значения, сопоставленного с ключом <tt>key</tt>. | ||
|} | |} | ||
== Демонстрация работы == | == Демонстрация работы == | ||
[http:// | * [http://www.cs.usfca.edu/~galles/visualization/BST.html Data Structure Visualizations — Binary Search Tree] | ||
* [http://visualgo.net/bst.html VisuAlgo — Binary Search Tree, AVL Tree] | |||
== Реализация == | == Реализация == | ||
| Строка 44: | Строка 46: | ||
int key; | int key; | ||
int value; | int value; | ||
TreeNode *left, *right; | |||
TreeNode (int k, int v | TreeNode(int k, int v) { | ||
key = k; | key = k; | ||
value = v; | |||
left = | left = right = NULL; | ||
} | } | ||
}; | }; | ||
Структура данных, являющаяся связной совокупностью таких узлов, называется двоичным деревом (англ. binary tree). Группа деревьев именуется лесом (англ. forest). | Структура данных, являющаяся связной ациклической совокупностью таких узлов, называется двоичным деревом (англ. binary tree). Группа деревьев именуется лесом (англ. forest). | ||
Пусть вершина A указывает на вершины B и C. Тогда B и C — ''потомки'' A, A — ''родитель'' B и C. Односвязный список имеет начальный элемент; по аналогии, двоичное дерево также имеет стартовую вершину — ''корень''. Из корня по указателям можно добраться до любой вершины дерева. Вершины, не имеющие потомков, называются ''листьями''. | Пусть вершина A указывает на вершины B и C. Тогда B и C — ''потомки'' A, A — ''родитель'' B и C. Односвязный список имеет начальный элемент; по аналогии, двоичное дерево также имеет стартовую вершину — ''корень''. Из корня по указателям можно добраться до любой вершины дерева. Вершины, не имеющие потомков, называются ''листьями''. | ||
Когда речь идёт о двоичном дереве поиска (англ. binary search tree, BST), подразумевается дерево, на элементы которого наложены дополнительные ограничения по размещению. Мы уже сталкивались с подобным: двоичное дерево, в котором ключ вершины не меньше, чем ключи её потомков, именуется [[АТД «Очередь с приоритетами»#Определение пирамиды|пирамидой]]. В пирамиде непосредственные потомки узла являются равноправными; в двоичном дереве поиска выделяется ''левый потомок'' и ''правый потомок'', и дополнительное ограничение сформулировано следующим образом: ключи в левом поддереве | Когда речь идёт о двоичном дереве поиска (англ. binary search tree, BST), подразумевается дерево, на элементы которого наложены дополнительные ограничения по размещению. Мы уже сталкивались с подобным: двоичное дерево, в котором ключ вершины не меньше, чем ключи её потомков, именуется [[АТД «Очередь с приоритетами»#Определение пирамиды|пирамидой]]. В пирамиде непосредственные потомки узла являются равноправными; в двоичном дереве поиска выделяется ''левый потомок'' и ''правый потомок'', и дополнительное ограничение сформулировано следующим образом: ключи в левом поддереве меньше ключа в родителе, а ключи в правом поддереве не меньше ключа в родителе (''основное свойство дерева поиска''). | ||
{| align="center" | |||
|+ '''Примеры двоичных деревьев поиска''' | |||
| [[Файл:bst_example_1.png|thumb|180px|Основные определения]] | |||
| [[Файл:bst_example_2.png|thumb|180px]] | |||
| [[Файл:bst_example_3.png|thumb|180px|Полностью заполненное дерево и вырожденное дерево]] | |||
|} | |||
=== Поиск в двоичном дереве === | === Поиск в двоичном дереве === | ||
Пусть имеется указатель на корень дерева <tt>TreeNode *root</tt> и требуется найти элемент с ключом <tt> | [[Файл:bst_search.png|thumb|right|360px|Поиск в двоичном дереве: сверху — успешный поиск ключа 31, снизу — поиск отсутствующего ключа 23]] | ||
Пусть имеется указатель на корень дерева <tt>TreeNode *root</tt> и требуется найти элемент с ключом <tt>key</tt>. Ключ <tt>key</tt> можно сравнить с <tt>root->key</tt>, и если повезёт, то требуемый элемент будет найден. В противном случае можно однозначно сказать, в каком из поддеревьев <tt>root</tt> может находиться элемент с ключом <tt>key</tt>: если <tt>key < root->key</tt>, то его следует искать в поддереве <tt>root->left</tt>, иначе — в <tt>root->right</tt>. Рассматриваемое поддерево имеет все свойства исходного двоичного дерева, поэтому действия по поиску можно повторить рекурсивно. Очевидно, что поиск завершается в одном из двух случаев: либо элемент найден, либо текущее поддерево стало пустым, т. е. поиск спустился до листьев и не встретил нужного элемента. | |||
{| width=" | {| | ||
| Рекурсивная реализация: | | width="50%" | Рекурсивная реализация: | ||
| width="10px" | | |||
| width="50%" | Итеративная реализация: | |||
|- | |- | ||
| | | | ||
TreeNode *find(TreeNode *n, int | TreeNode *find(TreeNode *n, int key) { | ||
if (n == NULL || | if (n == NULL || key == n->key) | ||
return n; | return n; | ||
if ( | if (key < n->key) | ||
return find(n->left, | return find(n->left, key); | ||
else | else | ||
return find(n->right, | return find(n->right, key); | ||
} | |||
int find(int key) { | |||
TreeNode *n = find(root, key); | |||
if (n != NULL) | |||
return n->value; | |||
else | |||
return -1; | |||
} | } | ||
| | | | ||
| | | | ||
int find(int key) { | |||
while (n != NULL && | TreeNode *n = root; | ||
if ( | while (n != NULL && key != n->key) { | ||
if (key < n->key) | |||
n = n->left; | n = n->left; | ||
else | else | ||
n = n->right; | n = n->right; | ||
return n; | } | ||
if (n != NULL) | |||
return n->value; | |||
else | |||
return -1; | |||
} | } | ||
|} | |} | ||
Обратите внимание на то, что поиск может завершиться неудачей, и тогда нужно возвращать такое значение, которое могло бы явно об этом сигнализировать. | |||
Худшим случаем для операции поиска является отсутствие нужного элемента в дереве. Тогда поиск спускается от корня до листа и затем возвращает значение <tt>NULL</tt>. Будем называть ''высотой дерева h'' количество вершин (или их связей, что на единицу меньше) на самом длинном пути от корня до какого-либо из листьев. Очевидно, что сложность операции поиска составляет O(h). | Худшим случаем для операции поиска является отсутствие нужного элемента в дереве. Тогда поиск спускается от корня до листа и затем возвращает значение <tt>NULL</tt>. Будем называть ''высотой дерева h'' количество вершин (или их связей, что на единицу меньше) на самом длинном пути от корня до какого-либо из листьев. Очевидно, что сложность операции поиска составляет O(h). | ||
=== Вставка в двоичное дерево поиска === | === Вставка в двоичное дерево поиска === | ||
[[Файл:bst_insert.png|thumb|right|360px|Вставка ключа 45 в двоичное дерево поиска]] | |||
Каждый добавляемый элемент должен располагаться на строго определённом месте, чтобы не нарушалось основное свойство двоичного дерева поиска. Найти такое место для конкретного элемента нам поможет та же идея, что была применена в реализации поиска. | Каждый добавляемый элемент должен располагаться на строго определённом месте, чтобы не нарушалось основное свойство двоичного дерева поиска. Найти такое место для конкретного элемента нам поможет та же идея, что была применена в реализации поиска. | ||
Будем идти от корня, спускаясь в те поддеревья, которые должны содержать добавляемый ключ. Когда спуск достигает значения <tt>NULL</tt>, остаётся только заменить указатель на это значение указателем на новый элемент. | Будем идти от корня, спускаясь в те поддеревья, которые должны содержать добавляемый ключ. Когда спуск достигает значения <tt>NULL</tt>, остаётся только заменить указатель на это значение указателем на новый элемент. | ||
{| | |||
| width="50%" | Рекурсивная реализация: | |||
| width="10px" | | |||
| width="50%" | Итеративная реализация: | |||
|- | |||
| | |||
void insert(TreeNode *&n, int key, int value) { | |||
if (n == NULL) | |||
n = new TreeNode(key, value); | |||
else if (key < n->key) | |||
insert(n->left, key, value); | |||
else | |||
insert(n->right, key, value); | |||
} | |||
void insert(int key, int value) { | |||
insert(root, key, value); | |||
} | |||
| | |||
| | |||
void insert(int key, int value) { | void insert(int key, int value) { | ||
if (root == NULL) { | if (root == NULL) { | ||
root = new TreeNode(key, value | root = new TreeNode(key, value); | ||
return; | return; | ||
} | } | ||
TreeNode *n = root; | TreeNode *n = root, *&child; | ||
while (true) { | while (true) { | ||
if (key < | if (key < n->key) | ||
child = n->left; | |||
else | |||
child = n->right; | |||
} | if (child == NULL) { | ||
child = new TreeNode(key, value); | |||
return; | |||
} else | |||
n = child; | |||
} | |||
} | |||
} else { | |} | ||
Таким образом, добавляемый элемент всегда становится листом двоичного дерева поиска. Достаточно очевидно, что вычислительная сложность операции вставки равна O(h). | |||
Порядок добавления элементов в двоичное дерево поиска играет очень важную роль. Минимальная высота двоичного дерева поиска, содержащего N элементов, равна ⌈log<sub>2</sub>N⌉; в этом случае заполнение дерева элементами равномерно, высоты поддеревьев любой вершины различаются не более чем на единицу, а само дерево именуется сбалансированным. Но существует и обратный случай, когда каждое добавление элемента увеличивает высоту дерева на 1, в результате дерево вырождается в односвязный список, а его высота становится равной N. Итоговая форма дерева зависит только от порядка добавления элементов. | |||
Обыкновенное двоичное дерево поиска не содержит никаких средств ограничения собственной высоты. Однако существует большое количество расширений двоичных деревьев, позволяющих поддерживать высоту на уровне O(logN), в которых, таким образом, операции поиска и добавления будут иметь сложность O(logN). Такие структуры данных называются ''балансирующимися деревьями''. Некоторые из них описаны в [[:Категория:Балансирующиеся деревья|соответствующем разделе]]. | |||
=== Удаление из двоичного дерева поиска === | |||
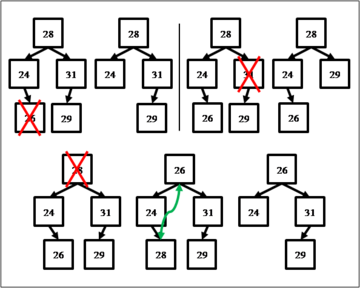
[[Файл:bst_remove.png|thumb|right|360px|Базовые случаи удаления элемента из двоичного дерева поиска]] | |||
Расположение элемента, который требуется удалить, определяется тем же методом, что был использован в процедурах поиска и вставки. Однако далее возможны различные варианты действий: | |||
*Если удаляемый элемент является листом (не имеет потомков), то достаточно убрать ссылку на него из его родителя; | |||
*Если удаляемый элемент имеет только одного потомка, то ссылка на удаляемый элемент в родителе заменяется ссылкой на этого потомка; | |||
*Наконец, наиболее нетривиальной является ситуация, когда удаляемый элемент имеет двух потомков. Рассмотрим её отдельно. | |||
Конечно, можно подвесить одно из поддеревьев к листу второго и далее рассматривать случай удаления узла с одним потомком, но такой подход увеличивает высоту дерева. Поэтому используется другое решение: удаляемый узел заменяется некоторым из его потомков (не обязательно непосредственных). | |||
Чтобы при этом не нарушилось основное свойство двоичного дерева, ключ этого потомка должен быть больше всех ключей левого поддерева удаляемого узла и не больше всех ключей правого поддерева удаляемого узла. Как можно догадаться, этому условию удовлетворяет только один потомок — узел с минимальным ключом в правом поддереве, т. е. узел, непосредственно следующий за удаляемым. Найти его можно, переходя по левым ссылкам в поддереве <tt>n->right</tt>, где <tt>n</tt> — удаляемый элемент. Далее производится обмен этих узлов и уничтожение ссылки на удаляемый узел. | |||
Можно видеть, что операция удаления элемента из двоичного дерева является достаточно сложной, и, кроме того, она реорганизует дерево, что в некоторых случаях является нежелательным. Поэтому часто удаление элемента заменяется присвоением ему некоторого «признака отсутствия», который позволяет игнорировать этот элемент в операциях поиска. | |||
Ниже приведён пример рекурсивной реализации удаления элемента. Вспомогательная функция <tt>successor()</tt> определяет непосредственный последующий узел для заданного узла, имеющего двух потомков. | |||
TreeNode *successor(TreeNode *n) { | |||
TreeNode *r = n->right; | |||
while (r->left != NULL) | |||
r = r->left; | |||
return r; | |||
} | |||
void remove(TreeNode *&n, int key) { | |||
if (n == NULL) | |||
return; | |||
if (key == n->key) { | |||
if (n->left == NULL || n->right == NULL) { | |||
TreeNode *child = (n->left != NULL ? n->left : n->right); | |||
delete n; | |||
n = child; | |||
} else { | |||
TreeNode *succ = successor(n); | |||
n->key = succ->key; | |||
n->value = succ->value; | |||
remove(n->right, succ->key); | |||
} | } | ||
return; | |||
} | |||
if (key < n->key) | |||
remove(n->left, key); | |||
else | |||
remove(n->right, key); | |||
} | |||
void remove(int key) { | |||
remove(root, key); | |||
} | |||
Вычислительная сложность операции удаления составляет O(h). | |||
=== Рекурсивный обход двоичного дерева поиска === | |||
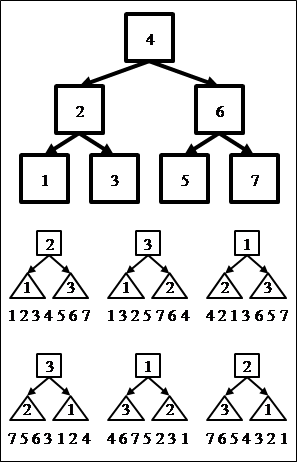
[[Файл:bst_traverses.png|thumb|right|Возможные рекурсивные обходы двоичного дерева]] | |||
Пусть требуется посетить все элементы двоичного дерева (например, чтобы вывести их). Приведём простую рекурсивную процедуру, решающую данную задачу: | |||
void traverse(TreeNode *n) { | |||
if (n == NULL) | |||
return; | |||
traverse(n->left); | |||
printf("%d", n->value); | |||
traverse(n->right); | |||
} | |||
Обход запускается вызовом <tt>traverse(root)</tt>. Приведённая реализация обеспечивает сначала посещение всех узлов, ключи которых не превышают ключа данного узла, затем посещение самого узла, затем посещение всех узлов, ключи которых больше ключа данного узла. Индуктивным рассуждением можно доказать, что данный обход выводит все элементы дерева в порядке увеличения их ключей. | |||
Данный обход (левое поддерево — родитель — правое поддерево) является лишь одним из шести возможных. На иллюстрации приведены результаты каждого типа обхода для одного и того же дерева. | |||
---- | |||
Ниже приведён код реализации словаря на двоичном дереве поиска. Ключами и значениями являются целые числа. Операция удаления опущена. | |||
class Map { | |||
struct TreeNode { | |||
int key; | |||
int value; | |||
TreeNode *left, *right; | |||
TreeNode(int k, int v) { | |||
key = k; | |||
value = v; | |||
left = right = NULL; | |||
} | |||
} root; | |||
TreeNode *find(TreeNode *n, int key) { | |||
if (n == NULL || key == n->key) | |||
return n; | |||
return find((key < n->key ? n->left : n->right), key); | |||
} | } | ||
void insert(TreeNode *n, int key, int value) { | |||
if (n == NULL) | |||
n = new TreeNode(key, value); | |||
if (key < n->key) | |||
n->left = insert(n->left, key, value); | |||
else | |||
n->right = insert(n->left, key, value); | |||
} | |||
public: | |||
Map() { | |||
root = NULL; | |||
} | |||
int find(int key) { | |||
TreeNode *n = find(root, key); | |||
return (n != NULL ? n->value : -1); | |||
} | |||
void insert(int key, int value) { | |||
insert(root, key, value); | |||
} | |||
}; | |||
Некоторые вопросы для размышления: | |||
*''Как реализовать отыскание максимума (минимума) в двоичном дереве поиска? Можно ли организовать очередь с приоритетами на двоичном дереве поиска?'' | |||
*''Как, в общем случае, реализовать операции поиска элемента, предшествующего данному, и элемента, следующего за данным?'' | |||
== Множество на деревьях поиска в STL == | |||
В стандартной библиотеке шаблонов C++ присутствует шаблон [http://www.cplusplus.com/reference/set/set/ <tt>set<T></tt>]. Для возможности его использования требуется подключить заголовочный файл <tt><set></tt> и пространство имён <tt>std</tt>. В том же заголовочном файле описан шаблон [http://www.cplusplus.com/reference/set/multiset/ <tt>multiset<T></tt>], представляющий множество, в котором могут храниться несколько одинаковых значений. Оба шаблона обычно реализованы на балансирующихся двоичных деревьях поиска. | |||
#include <iostream> | |||
#include <set> | |||
using namespace std; | |||
int main() { | |||
set<int> s; | |||
for (int i = 1; i < 6; i++) | |||
s.insert(i * i); | |||
for (int i = 0; i < 30; i++) { | |||
if (s.find(i) != s.end()) | |||
cout << i << ' '; | |||
return 0; //результат "1 4 9 16 25" | |||
} | } | ||
STL предоставляет следующий набор методов для множества (тип <tt>It</tt> обозначает итератор, тип <tt>size_t</tt> — беззнаковое целое): | |||
{| class="methodlist" | |||
| || || set<T>() || — конструктор множества; поддерживается инициализация парой итераторов; | |||
|- | |||
| || pair<It, bool> || insert(T x) || — добавление значения <tt>x</tt> в множество. Метод возвращает пару, первый элемент которой указывает на элемент со значением <tt>val</tt>, а второй равен <tt>true</tt>, если элемент был добавлен, либо <tt>false</tt>, если такой элемент уже был в множестве. Эквивалент этого метода для шаблона <tt>multiset</tt> возвращает только итератор, указывающий на добавленный элемент; | |||
|- | |||
| || size_t || erase(T x) || — исключение значения <tt>x</tt> из множества. Возвращает количество исключённых элементов. Метод также поддерживает удаление элемента на определённой позиции, если передать ему не значение, а итератор (или пару итераторов); | |||
|- | |||
| || It || find(T x) || — поиск элемента <tt>x</tt> в множестве. Метод возвращает итератор, указывающий на найденный элемент, либо итератор <tt>set::end()</tt>, если элемент не был найден; | |||
|- | |||
| || size_t || count(T x) || — подсчёт количества элементов, равных <tt>x</tt>; | |||
|- | |||
| || size_t || size() || — получение количества элементов в множестве; | |||
|- | |||
| || size_t || max_size() || — получение максимального возможного (для данного компьютера и реализации STL) количества элементов в множестве; | |||
|- | |||
| || bool || empty() || — проверка множества на пустоту; | |||
|- | |||
| || void || clear() || — очистка множества (исключение всех элементов); | |||
|- | |||
| || It || lower_bound(T x) || — получение итератора, указывающего на минимальный элемент, не меньший <tt>x</tt>. Если такого элемента нет, возвращается итератор <tt>set::end()</tt>; | |||
|- | |||
| || It || upper_bound(T x) || — получение итератора, указывающего на минимальный элемент, больший <tt>x</tt>. Если такого элемента нет, возвращается итератор <tt>set::end()</tt>; | |||
|- | |||
| || pair<It, It> || equal_range(T x) || — получение пары итераторов, аналогичных результатам двух описанных выше методов. | |||
|} | |||
Элементы внутри <tt>set</tt> и <tt>multiset</tt> являются упорядоченными по возрастанию. | |||
== Словарь на деревьях поиска в STL == | |||
В стандартной библиотеке шаблонов C++ присутствует шаблон [http://www.cplusplus.com/reference/map/map/ <tt>map<T1, T2></tt>]. Для возможности его использования требуется подключить заголовочный файл <tt><map></tt> и пространство имён <tt>std</tt>. В том же заголовочном файле описан шаблон [http://www.cplusplus.com/reference/map/multimap/ <tt>multimap<T1, T2></tt>], представляющий словарь, в котором могут храниться несколько пар с одинаковыми ключами. Оба шаблона обычно реализованы на балансирующихся двоичных деревьях поиска. | |||
#include <iostream> | |||
#include <string> | |||
#include <map> | |||
using namespace std; | |||
int main() { | |||
map<int, string> m; | |||
m.insert(make_pair(1828, "Tolstoy")); | |||
m.insert(make_pair(1799, "Pushkin")); | |||
m.insert(make_pair(1821, "Dostoevsky")); | |||
map<int, string>::iterator it, end; | |||
it = m.lower_bound(1750); | |||
end = m.upper_bound(1850); | |||
for (; it != end; it++) { | |||
cout << it->second << "(" << it->first << ") "; | |||
} | |||
return 0; //результат "Pushkin (1799) Dostoevsky (1821) Tolstoy (1828) " | |||
} | |||
STL предоставляет следующий набор методов для множества (тип <tt>It</tt> обозначает итератор, тип <tt>size_t</tt> — беззнаковое целое): | |||
{| class="methodlist" | |||
| || || map<T1, T2>() || — конструктор словаря. Типом ключей является <tt>T1</tt>, типом значений — <tt>T2</tt>. Поддерживается инициализация парой итераторов; | |||
|- | |||
| || pair<It, bool> || insert(pair<T1, T2> x) || — добавление пары <tt>x</tt> в словарь. Метод принимает именно пару (которая может быть создана методом <tt>std::make_pair()</tt>), а не два отдельных аргумента. Операция вставки возвращает пару, аналогичную возвращаемой методом <tt>set::insert()</tt>; | |||
|- | |||
| || size_t || erase(T1 k) || — исключение из словаря элементов с ключом <tt>k</tt>. Возвращает количество исключённых элементов. Метод также поддерживает удаление элемента на определённой позиции, если передать ему не значение, а итератор (или пару итераторов); | |||
|- | |||
| || It || find(T1 k) || — поиск элемента с ключом <tt>k</tt> в словаре. Метод возвращает итератор, указывающий на найденную пару (именно пару, обратите на это внимание), либо итератор <tt>set::end()</tt>, если элемент не был найден; | |||
|- | |||
| || size_t || count(T1 k) || — подсчёт количества пар, ключи которых равны <tt>k</tt>; | |||
|- | |||
| || size_t || size() || — получение количества пар в словаре; | |||
|- | |||
| || size_t || max_size() || — получение максимального возможного (для данного компьютера и реализации STL) количества элементов в множестве; | |||
|- | |||
| || bool || empty() || — проверка словаря на пустоту; | |||
|- | |||
| || void || clear() || — очистка словаря (исключение всех элементов); | |||
|- | |||
| || It || lower_bound(T1 k) || — получение итератора, указывающего на пару с минимальным ключом, не меньшим <tt>k</tt>. Если такой пары нет, возвращается итератор <tt>set::end()</tt>; | |||
|- | |||
| || It || upper_bound(T1 k) || — получение итератора, указывающего на пару с минимальным ключом, большим <tt>k</tt>. Если такой пары нет, возвращается итератор <tt>set::end()</tt>; | |||
|- | |||
| || pair<It, It> || equal_range(T1 k) || — получение пары итераторов, аналогичных результатам двух описанных выше методов. | |||
|} | |||
Элементы внутри <tt>map</tt> и <tt>multimap</tt> упорядочены по возрастанию ключей. | |||
== Ссылки == | |||
Теория: | |||
* [http://neerc.ifmo.ru/wiki/index.php?title=%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D0%BF%D0%BE%D0%B8%D1%81%D0%BA%D0%B0,_%D0%BD%D0%B0%D0%B8%D0%B2%D0%BD%D0%B0%D1%8F_%D1%80%D0%B5%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F neerc.ifmo.ru/wiki — Дерево поиска, наивная реализация] | |||
* [http://algs4.cs.princeton.edu/lectures/32BinarySearchTrees.pdf algs4.cs.princeton.edu/lectures — 3.2 Binary Search Trees] | |||
Код: | |||
* [http://github.com/indy256/codelibrary/blob/master/java/src/BinarySearchTree.java CodeLibrary — Binary Search Tree] | |||
* [http://algs4.cs.princeton.edu/code/edu/princeton/cs/algs4/BST.java.html algs4.cs.princeton.edu/code — binary search tree] | |||
Задачи: | |||
* [http://informatics.mccme.ru/course/view.php?id=18 informatics.mccme.ru — Курс «Структуры данных» — часть 3] | |||
* [[:Категория: Задачи: map|Задачи: map]] | |||
[[Category:Базовые структуры и абстрактные типы данных]] | |||
Текущая версия от 15:05, 24 мая 2023
TLDR
Общие сведения
Иногда решение задачи требует применения абстрактного типа данных «Множество», однако отсутствует возможность отмечать каждое допустимое значение отдельной логической переменной (если множество имеет большую мощность или бесконечно, как, например, множество строк или вещественных чисел). В этом случае необходима такая реализация множества, которая явно хранит выбранные элементы внутри себя, а также позволяет оперативно их отыскивать, добавлять и удалять. Такие требования роднят множество с другим типом данных, именуемым словарём.
Словарь (англ. dictionary, map) — абстрактный тип данных, позволяющий хранить набор значений, обращение к которым происходит по ключам. Ключи должны допускать сравнение друг с другом. Примеры словарей достаточно разнообразны:
- Обычный толковый словарь хранит определения слов (являющиеся значениями), сопоставленные с самими словами (являющимися ключами);
- Банковская база данных может хранить данные клиентов, сопоставленные с номерами счетов;
- Экзаменационная ведомость содержит оценки, сопоставленные с фамилиями студентов, и т. д.
Множество можно рассматривать как словарь, в котором ключ элемента совпадает с его значением. Массив можно рассматривать как словарь, в котором ключи являются целыми числами. С другой стороны, словарь можно рассматривать как массив, тип индексов которого может не быть целочисленным. Например, содержимое телефонного справочника можно рассматривать как массив телефонных номеров, индексами в котором являются фамилии абонентов. Отсюда другое название словаря — ассоциативный массив (англ. assotiative array).
Как и для случая множеств, возможна такая реализация словаря, в которой каждому ключу могут быть сопоставлены несколько значений (тогда для обозначения применяется термин multimap).
Интерфейс
Стандартный интерфейс множества был рассмотрен в статье «Множество (реализация на битовых векторах)». Операции словаря похожи на операции множества, но в качестве параметров принимают ключи, а не непосредственные значения элементов.
| void | insert(T1 key, T2 value) | — добавление пары (key, value) в словарь; | |
| void | remove(T1 key) | — исключение из словаря значения, сопоставленного с ключом key; | |
| T2 | find(T1 key) | — получение значения, сопоставленного с ключом key. |
Демонстрация работы
Реализация
Как упоминалось ранее, словарь должен хранить все добавленные в него пары (ключ — значение). Можно предложить несколько подходов к организации этой информации внутри словаря:
- Неупорядоченный массив пар. В этом случае добавление пары в конец массива имеет сложность O(1), поиск по ключу требует просмотра всего массива (O(N)), удаление также может потребовать сдвига всех элементов (O(N)).
- Отсортированный по ключам массив пар. Добавление пары в нужное место может потребовать сдвига всех элементов (O(N)), бинарный поиск по ключу требует O(logN), удаление может потребовать сдвига всех элементов (O(N)).
- Список пар позволит производить добавление и удаление за O(1), но поиск будет требовать O(N).
Можно видеть, что все предложенные варианты содержат операции с линейным временем работы, которое серьёзно ограничивает область их применения. Тем не менее, возможен подход, который позволяет достичь вычислительной сложности Ω(logN) для каждой из операций. Этот подход основан на применении структур данных, называемых деревьями поиска.
Определение двоичного дерева поиска
Структура, представляющая элемент односвязного списка, имела два основных поля: хранимое значение и указатель на следующую подобную структуру. Пусть число указателей в узле равно двум. Тогда каждый такой узел может иметь не более двух потомков. Пусть также хранимая информация представлена в виде пары (ключ — значение).
struct TreeNode {
int key;
int value;
TreeNode *left, *right;
TreeNode(int k, int v) {
key = k;
value = v;
left = right = NULL;
}
};
Структура данных, являющаяся связной ациклической совокупностью таких узлов, называется двоичным деревом (англ. binary tree). Группа деревьев именуется лесом (англ. forest).
Пусть вершина A указывает на вершины B и C. Тогда B и C — потомки A, A — родитель B и C. Односвязный список имеет начальный элемент; по аналогии, двоичное дерево также имеет стартовую вершину — корень. Из корня по указателям можно добраться до любой вершины дерева. Вершины, не имеющие потомков, называются листьями.
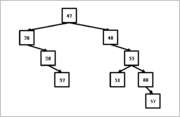
Когда речь идёт о двоичном дереве поиска (англ. binary search tree, BST), подразумевается дерево, на элементы которого наложены дополнительные ограничения по размещению. Мы уже сталкивались с подобным: двоичное дерево, в котором ключ вершины не меньше, чем ключи её потомков, именуется пирамидой. В пирамиде непосредственные потомки узла являются равноправными; в двоичном дереве поиска выделяется левый потомок и правый потомок, и дополнительное ограничение сформулировано следующим образом: ключи в левом поддереве меньше ключа в родителе, а ключи в правом поддереве не меньше ключа в родителе (основное свойство дерева поиска).
Поиск в двоичном дереве
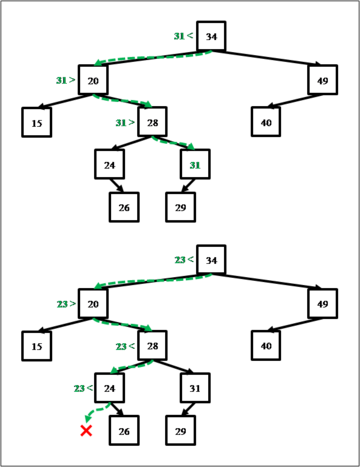
Пусть имеется указатель на корень дерева TreeNode *root и требуется найти элемент с ключом key. Ключ key можно сравнить с root->key, и если повезёт, то требуемый элемент будет найден. В противном случае можно однозначно сказать, в каком из поддеревьев root может находиться элемент с ключом key: если key < root->key, то его следует искать в поддереве root->left, иначе — в root->right. Рассматриваемое поддерево имеет все свойства исходного двоичного дерева, поэтому действия по поиску можно повторить рекурсивно. Очевидно, что поиск завершается в одном из двух случаев: либо элемент найден, либо текущее поддерево стало пустым, т. е. поиск спустился до листьев и не встретил нужного элемента.
| Рекурсивная реализация: | Итеративная реализация: | |
TreeNode *find(TreeNode *n, int key) {
if (n == NULL || key == n->key)
return n;
if (key < n->key)
return find(n->left, key);
else
return find(n->right, key);
}
int find(int key) {
TreeNode *n = find(root, key);
if (n != NULL)
return n->value;
else
return -1;
}
|
int find(int key) {
TreeNode *n = root;
while (n != NULL && key != n->key) {
if (key < n->key)
n = n->left;
else
n = n->right;
}
if (n != NULL)
return n->value;
else
return -1;
}
|
Обратите внимание на то, что поиск может завершиться неудачей, и тогда нужно возвращать такое значение, которое могло бы явно об этом сигнализировать.
Худшим случаем для операции поиска является отсутствие нужного элемента в дереве. Тогда поиск спускается от корня до листа и затем возвращает значение NULL. Будем называть высотой дерева h количество вершин (или их связей, что на единицу меньше) на самом длинном пути от корня до какого-либо из листьев. Очевидно, что сложность операции поиска составляет O(h).
Вставка в двоичное дерево поиска
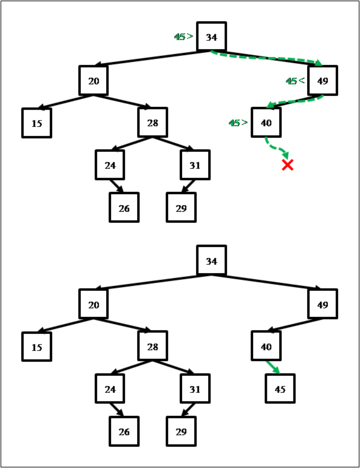
Каждый добавляемый элемент должен располагаться на строго определённом месте, чтобы не нарушалось основное свойство двоичного дерева поиска. Найти такое место для конкретного элемента нам поможет та же идея, что была применена в реализации поиска.
Будем идти от корня, спускаясь в те поддеревья, которые должны содержать добавляемый ключ. Когда спуск достигает значения NULL, остаётся только заменить указатель на это значение указателем на новый элемент.
| Рекурсивная реализация: | Итеративная реализация: | |
void insert(TreeNode *&n, int key, int value) {
if (n == NULL)
n = new TreeNode(key, value);
else if (key < n->key)
insert(n->left, key, value);
else
insert(n->right, key, value);
}
void insert(int key, int value) {
insert(root, key, value);
}
|
void insert(int key, int value) {
if (root == NULL) {
root = new TreeNode(key, value);
return;
}
TreeNode *n = root, *&child;
while (true) {
if (key < n->key)
child = n->left;
else
child = n->right;
if (child == NULL) {
child = new TreeNode(key, value);
return;
} else
n = child;
}
}
|
Таким образом, добавляемый элемент всегда становится листом двоичного дерева поиска. Достаточно очевидно, что вычислительная сложность операции вставки равна O(h).
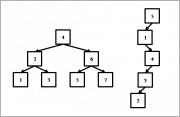
Порядок добавления элементов в двоичное дерево поиска играет очень важную роль. Минимальная высота двоичного дерева поиска, содержащего N элементов, равна ⌈log2N⌉; в этом случае заполнение дерева элементами равномерно, высоты поддеревьев любой вершины различаются не более чем на единицу, а само дерево именуется сбалансированным. Но существует и обратный случай, когда каждое добавление элемента увеличивает высоту дерева на 1, в результате дерево вырождается в односвязный список, а его высота становится равной N. Итоговая форма дерева зависит только от порядка добавления элементов.
Обыкновенное двоичное дерево поиска не содержит никаких средств ограничения собственной высоты. Однако существует большое количество расширений двоичных деревьев, позволяющих поддерживать высоту на уровне O(logN), в которых, таким образом, операции поиска и добавления будут иметь сложность O(logN). Такие структуры данных называются балансирующимися деревьями. Некоторые из них описаны в соответствующем разделе.
Удаление из двоичного дерева поиска
Расположение элемента, который требуется удалить, определяется тем же методом, что был использован в процедурах поиска и вставки. Однако далее возможны различные варианты действий:
- Если удаляемый элемент является листом (не имеет потомков), то достаточно убрать ссылку на него из его родителя;
- Если удаляемый элемент имеет только одного потомка, то ссылка на удаляемый элемент в родителе заменяется ссылкой на этого потомка;
- Наконец, наиболее нетривиальной является ситуация, когда удаляемый элемент имеет двух потомков. Рассмотрим её отдельно.
Конечно, можно подвесить одно из поддеревьев к листу второго и далее рассматривать случай удаления узла с одним потомком, но такой подход увеличивает высоту дерева. Поэтому используется другое решение: удаляемый узел заменяется некоторым из его потомков (не обязательно непосредственных).
Чтобы при этом не нарушилось основное свойство двоичного дерева, ключ этого потомка должен быть больше всех ключей левого поддерева удаляемого узла и не больше всех ключей правого поддерева удаляемого узла. Как можно догадаться, этому условию удовлетворяет только один потомок — узел с минимальным ключом в правом поддереве, т. е. узел, непосредственно следующий за удаляемым. Найти его можно, переходя по левым ссылкам в поддереве n->right, где n — удаляемый элемент. Далее производится обмен этих узлов и уничтожение ссылки на удаляемый узел.
Можно видеть, что операция удаления элемента из двоичного дерева является достаточно сложной, и, кроме того, она реорганизует дерево, что в некоторых случаях является нежелательным. Поэтому часто удаление элемента заменяется присвоением ему некоторого «признака отсутствия», который позволяет игнорировать этот элемент в операциях поиска.
Ниже приведён пример рекурсивной реализации удаления элемента. Вспомогательная функция successor() определяет непосредственный последующий узел для заданного узла, имеющего двух потомков.
TreeNode *successor(TreeNode *n) {
TreeNode *r = n->right;
while (r->left != NULL)
r = r->left;
return r;
}
void remove(TreeNode *&n, int key) {
if (n == NULL)
return;
if (key == n->key) {
if (n->left == NULL || n->right == NULL) {
TreeNode *child = (n->left != NULL ? n->left : n->right);
delete n;
n = child;
} else {
TreeNode *succ = successor(n);
n->key = succ->key;
n->value = succ->value;
remove(n->right, succ->key);
}
return;
}
if (key < n->key)
remove(n->left, key);
else
remove(n->right, key);
}
void remove(int key) {
remove(root, key);
}
Вычислительная сложность операции удаления составляет O(h).
Рекурсивный обход двоичного дерева поиска
Пусть требуется посетить все элементы двоичного дерева (например, чтобы вывести их). Приведём простую рекурсивную процедуру, решающую данную задачу:
void traverse(TreeNode *n) {
if (n == NULL)
return;
traverse(n->left);
printf("%d", n->value);
traverse(n->right);
}
Обход запускается вызовом traverse(root). Приведённая реализация обеспечивает сначала посещение всех узлов, ключи которых не превышают ключа данного узла, затем посещение самого узла, затем посещение всех узлов, ключи которых больше ключа данного узла. Индуктивным рассуждением можно доказать, что данный обход выводит все элементы дерева в порядке увеличения их ключей.
Данный обход (левое поддерево — родитель — правое поддерево) является лишь одним из шести возможных. На иллюстрации приведены результаты каждого типа обхода для одного и того же дерева.
Ниже приведён код реализации словаря на двоичном дереве поиска. Ключами и значениями являются целые числа. Операция удаления опущена.
class Map {
struct TreeNode {
int key;
int value;
TreeNode *left, *right;
TreeNode(int k, int v) {
key = k;
value = v;
left = right = NULL;
}
} root;
TreeNode *find(TreeNode *n, int key) {
if (n == NULL || key == n->key)
return n;
return find((key < n->key ? n->left : n->right), key);
}
void insert(TreeNode *n, int key, int value) {
if (n == NULL)
n = new TreeNode(key, value);
if (key < n->key)
n->left = insert(n->left, key, value);
else
n->right = insert(n->left, key, value);
}
public:
Map() {
root = NULL;
}
int find(int key) {
TreeNode *n = find(root, key);
return (n != NULL ? n->value : -1);
}
void insert(int key, int value) {
insert(root, key, value);
}
};
Некоторые вопросы для размышления:
- Как реализовать отыскание максимума (минимума) в двоичном дереве поиска? Можно ли организовать очередь с приоритетами на двоичном дереве поиска?
- Как, в общем случае, реализовать операции поиска элемента, предшествующего данному, и элемента, следующего за данным?
Множество на деревьях поиска в STL
В стандартной библиотеке шаблонов C++ присутствует шаблон set<T>. Для возможности его использования требуется подключить заголовочный файл <set> и пространство имён std. В том же заголовочном файле описан шаблон multiset<T>, представляющий множество, в котором могут храниться несколько одинаковых значений. Оба шаблона обычно реализованы на балансирующихся двоичных деревьях поиска.
#include <iostream>
#include <set>
using namespace std;
int main() {
set<int> s;
for (int i = 1; i < 6; i++)
s.insert(i * i);
for (int i = 0; i < 30; i++) {
if (s.find(i) != s.end())
cout << i << ' ';
return 0; //результат "1 4 9 16 25"
}
STL предоставляет следующий набор методов для множества (тип It обозначает итератор, тип size_t — беззнаковое целое):
| set<T>() | — конструктор множества; поддерживается инициализация парой итераторов; | ||
| pair<It, bool> | insert(T x) | — добавление значения x в множество. Метод возвращает пару, первый элемент которой указывает на элемент со значением val, а второй равен true, если элемент был добавлен, либо false, если такой элемент уже был в множестве. Эквивалент этого метода для шаблона multiset возвращает только итератор, указывающий на добавленный элемент; | |
| size_t | erase(T x) | — исключение значения x из множества. Возвращает количество исключённых элементов. Метод также поддерживает удаление элемента на определённой позиции, если передать ему не значение, а итератор (или пару итераторов); | |
| It | find(T x) | — поиск элемента x в множестве. Метод возвращает итератор, указывающий на найденный элемент, либо итератор set::end(), если элемент не был найден; | |
| size_t | count(T x) | — подсчёт количества элементов, равных x; | |
| size_t | size() | — получение количества элементов в множестве; | |
| size_t | max_size() | — получение максимального возможного (для данного компьютера и реализации STL) количества элементов в множестве; | |
| bool | empty() | — проверка множества на пустоту; | |
| void | clear() | — очистка множества (исключение всех элементов); | |
| It | lower_bound(T x) | — получение итератора, указывающего на минимальный элемент, не меньший x. Если такого элемента нет, возвращается итератор set::end(); | |
| It | upper_bound(T x) | — получение итератора, указывающего на минимальный элемент, больший x. Если такого элемента нет, возвращается итератор set::end(); | |
| pair<It, It> | equal_range(T x) | — получение пары итераторов, аналогичных результатам двух описанных выше методов. |
Элементы внутри set и multiset являются упорядоченными по возрастанию.
Словарь на деревьях поиска в STL
В стандартной библиотеке шаблонов C++ присутствует шаблон map<T1, T2>. Для возможности его использования требуется подключить заголовочный файл <map> и пространство имён std. В том же заголовочном файле описан шаблон multimap<T1, T2>, представляющий словарь, в котором могут храниться несколько пар с одинаковыми ключами. Оба шаблона обычно реализованы на балансирующихся двоичных деревьях поиска.
#include <iostream>
#include <string>
#include <map>
using namespace std;
int main() {
map<int, string> m;
m.insert(make_pair(1828, "Tolstoy"));
m.insert(make_pair(1799, "Pushkin"));
m.insert(make_pair(1821, "Dostoevsky"));
map<int, string>::iterator it, end;
it = m.lower_bound(1750);
end = m.upper_bound(1850);
for (; it != end; it++) {
cout << it->second << "(" << it->first << ") ";
}
return 0; //результат "Pushkin (1799) Dostoevsky (1821) Tolstoy (1828) "
}
STL предоставляет следующий набор методов для множества (тип It обозначает итератор, тип size_t — беззнаковое целое):
| map<T1, T2>() | — конструктор словаря. Типом ключей является T1, типом значений — T2. Поддерживается инициализация парой итераторов; | ||
| pair<It, bool> | insert(pair<T1, T2> x) | — добавление пары x в словарь. Метод принимает именно пару (которая может быть создана методом std::make_pair()), а не два отдельных аргумента. Операция вставки возвращает пару, аналогичную возвращаемой методом set::insert(); | |
| size_t | erase(T1 k) | — исключение из словаря элементов с ключом k. Возвращает количество исключённых элементов. Метод также поддерживает удаление элемента на определённой позиции, если передать ему не значение, а итератор (или пару итераторов); | |
| It | find(T1 k) | — поиск элемента с ключом k в словаре. Метод возвращает итератор, указывающий на найденную пару (именно пару, обратите на это внимание), либо итератор set::end(), если элемент не был найден; | |
| size_t | count(T1 k) | — подсчёт количества пар, ключи которых равны k; | |
| size_t | size() | — получение количества пар в словаре; | |
| size_t | max_size() | — получение максимального возможного (для данного компьютера и реализации STL) количества элементов в множестве; | |
| bool | empty() | — проверка словаря на пустоту; | |
| void | clear() | — очистка словаря (исключение всех элементов); | |
| It | lower_bound(T1 k) | — получение итератора, указывающего на пару с минимальным ключом, не меньшим k. Если такой пары нет, возвращается итератор set::end(); | |
| It | upper_bound(T1 k) | — получение итератора, указывающего на пару с минимальным ключом, большим k. Если такой пары нет, возвращается итератор set::end(); | |
| pair<It, It> | equal_range(T1 k) | — получение пары итераторов, аналогичных результатам двух описанных выше методов. |
Элементы внутри map и multimap упорядочены по возрастанию ключей.
Ссылки
Теория:
- neerc.ifmo.ru/wiki — Дерево поиска, наивная реализация
- algs4.cs.princeton.edu/lectures — 3.2 Binary Search Trees
Код:
Задачи: