Декартово дерево: различия между версиями
Ctrlalt (обсуждение | вклад) Нет описания правки |
Ctrlalt (обсуждение | вклад) Нет описания правки |
||
| (не показана 41 промежуточная версия 2 участников) | |||
| Строка 1: | Строка 1: | ||
< | == TLDR == | ||
<youtube width="300" height="180">68mMGJl5F8s</youtube> | |||
<youtube width="300" height="180">WuuLjDIiJqc</youtube> | |||
<youtube width="300" height="180">8hNkIeTKCpk</youtube> | |||
== Общие сведения == | == Общие сведения == | ||
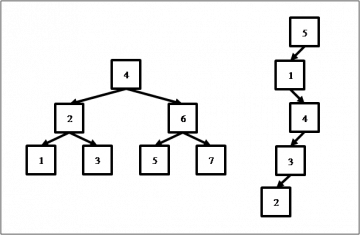
[[Файл: | [[Файл:bst_example_3.png|thumb|360px|Влияние порядка вставки элементов на форму дерева]] | ||
Вычислительная сложность большинства операций с двоичными деревьями поиска пропорциональна высоте дерева. Высота дерева определяется порядком добавления и удаления его элементов. Дерево, содержащее N элементов, может иметь высоту от ⌈log<sub>2</sub>N⌉ до N. | Вычислительная сложность большинства операций с двоичными деревьями поиска пропорциональна высоте дерева. Высота дерева определяется порядком добавления и удаления его элементов. Дерево, содержащее N элементов, может иметь высоту от ⌈log<sub>2</sub>N⌉ до N. | ||
Пусть каждый узел двоичного дерева поиска имеет, кроме ключа, дополнительное значение, именуемое ''приоритетом'', и установлено следующее дополнительное ограничение: элементы дерева по своим приоритетам формируют пирамиду, то есть приоритет каждого из узлов не меньше приоритетов его потомков (случай максимальной пирамиды). Тогда, вне зависимости от порядка операций с получившимся деревом, его форма задана однозначно. | Пусть каждый узел двоичного дерева поиска имеет, кроме ключа, дополнительное значение, именуемое ''приоритетом'', и установлено следующее дополнительное ограничение: элементы дерева по своим приоритетам формируют [[АТД «Очередь с приоритетами»#Определение пирамиды|пирамиду]], то есть приоритет каждого из узлов не меньше приоритетов его потомков (случай максимальной пирамиды). Тогда, вне зависимости от порядка операций с получившимся деревом, его форма задана однозначно. | ||
Убедиться в справедливости данного утверждения можно следующим образом. Корнем дерева является элемент с наибольшим приоритетом. В левом поддереве располагаются элементы, ключи которых не превышают ключа корня, в правом поддереве — остальные элементы (дерево продолжает оставаться деревом поиска). Рекурсивно рассматривая левое и правое поддеревья (корнями которых также являются их элементы с максимальными приоритетами, и так далее), приходим к выводу, что положение каждого элемента дерева задано однозначно, зависит от пары (ключ — приоритет) и не зависит от порядка добавления элементов в дерево. | Убедиться в справедливости данного утверждения можно следующим образом. Корнем дерева является элемент с наибольшим приоритетом. В левом поддереве располагаются элементы, ключи которых не превышают ключа корня, в правом поддереве — остальные элементы (дерево продолжает оставаться деревом поиска). Рекурсивно рассматривая левое и правое поддеревья (корнями которых также являются их элементы с максимальными приоритетами, и так далее), приходим к выводу, что положение каждого элемента дерева задано однозначно, зависит от пары (ключ — приоритет) и не зависит от порядка добавления элементов в дерево. | ||
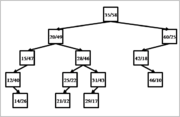
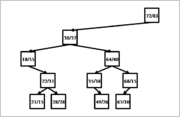
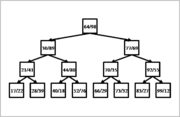
{| align="center" | |||
|+ '''Примеры декартовых деревьев''' | |||
| [[Файл:treap_example_1.png|thumb|180px]] | |||
| [[Файл:treap_example_2.png|thumb|180px]] | |||
| [[Файл:treap_example_3.png|thumb|180px]] | |||
|} | |||
[[Файл:treap_cartesian.png|thumb|right|Декартово дерево на декартовой плоскости]] | |||
Можно показать, что доля двоичных деревьев поиска из N элементов, высота которых не превышает ⌈4log<sub>2</sub>N⌉, стремится к 100%. Этот факт позволяет применить идею рандомизированного алгоритма: если приоритеты узлов назначаются при добавлении случайным образом, то вероятность того, что получившееся дерево будет иметь высоту, превышающую ⌈4log<sub>2</sub>N⌉, становится пренебрежимо малой. Таким образом, дерево поиска со случайными приоритетами, элементы которого формируют пирамиду по приоритетам, позволяет выполнять основные операции со сложностью O(logN). | Можно показать, что доля двоичных деревьев поиска из N элементов, высота которых не превышает ⌈4log<sub>2</sub>N⌉, стремится к 100%. Этот факт позволяет применить идею рандомизированного алгоритма: если приоритеты узлов назначаются при добавлении случайным образом, то вероятность того, что получившееся дерево будет иметь высоту, превышающую ⌈4log<sub>2</sub>N⌉, становится пренебрежимо малой. Таким образом, дерево поиска со случайными приоритетами, элементы которого формируют пирамиду по приоритетам, позволяет выполнять основные операции со сложностью O(logN). | ||
| Строка 18: | Строка 25: | ||
Описанная структура данных называется декартовым деревом (дерамидой, англ. cartesian tree, treap). Если пары (ключ — приоритет) рассматривать как координаты узла на декартовой плоскости, то любое нарисованное таким образом декартово дерево будет планарным (не будет иметь рёберных пересечений). | Описанная структура данных называется декартовым деревом (дерамидой, англ. cartesian tree, treap). Если пары (ключ — приоритет) рассматривать как координаты узла на декартовой плоскости, то любое нарисованное таким образом декартово дерево будет планарным (не будет иметь рёберных пересечений). | ||
== | == Интерфейс == | ||
[ | Декартовы деревья позволяют реализовать весь интерфейс обычных [[АТД «Множество» и «Словарь». Реализация на деревьях поиска#Определение двоичного дерева поиска|двоичных деревьев поиска]], однако позволяют (с высокой вероятностью) выполнять все операции со сложностью O(logN). | ||
{| class="methodlist" | |||
| || void || insert(T1 key, T2 value) || — добавление пары <tt>(key, value)</tt> в декартово дерево; | |||
|- | |||
| || void || remove(T1 key) || — исключение из дерева всех элементов, ключи которых равны <tt>key</tt>; | |||
|- | |||
| || T2 || find(T1 key) || — получение значения, сопоставленного с ключом <tt>key</tt>. | |||
|} | |||
Кроме того, на декартовых деревьях достаточно просто реализуются различные выборки и групповые модификации: | |||
{| class="methodlist" | |||
| || T2 || query(T1 key1, T1 key2) || — запрос некоторой функции (суммы, произведения, максимума и т. п.) для всех элементов, ключи которых принадлежат диапазону [<tt>key1</tt>; <tt>key2</tt>]; | |||
|- | |||
| || void || modify(T1 key1, T1 key2) || — групповая модификация (прибавление некоторой величины, умножение на некоторую величину, установка свойств и т. д.) для всех элементов, ключи которых принадлежат диапазону [<tt>key1</tt>; <tt>key2</tt>]. | |||
|} | |||
Следует отметить, что всё многообразие методов на декартовых деревьях основывается на двух базовых операциях, речь о которых пойдёт ниже — объединении дерамид и разрезании дерамиды по ключу. | |||
== Реализация базовых операций == | == Реализация базовых операций == | ||
| Строка 30: | Строка 55: | ||
k = key; | k = key; | ||
v = value; | v = value; | ||
p = | p = rand(); | ||
l = r = NULL; | l = r = NULL; | ||
} | } | ||
| Строка 36: | Строка 61: | ||
=== Слияние декартовых деревьев (merge) === | === Слияние декартовых деревьев (merge) === | ||
Пусть даны две дерамиды <tt>A</tt> (с корнем <tt>a</tt>) и <tt>B</tt> (с корнем <tt>b</tt>), причём все ключи элементов <tt>A</tt> меньше ключа любого элемента <tt>B</tt> (или не превышают его, в том случае, когда в дерамиде разрешены элементы с равными ключами). Требуется сформировать новую дерамиду <tt>T</tt> из элементов <tt>A</tt> и <tt>B</tt> и вернуть указатель на её корень. | |||
Пусть даны две дерамиды <tt>A</tt> (с корнем <tt>a</tt>) и <tt>B</tt> (с корнем <tt>b</tt>), причём ключи элементов <tt>A</tt> меньше | |||
TreapNode *merge(TreapNode *a, TreapNode *b) { | TreapNode *merge(TreapNode *a, TreapNode *b) { | ||
| Строка 51: | Строка 75: | ||
} | } | ||
Корнем <tt>T</tt> будет тот элемент <tt>A</tt> или <tt>B</tt>, приоритет которого является максимальным. Нетрудно заметить, что таковым элементом может быть либо <tt>a</tt>, либо <tt>b</tt>. Пусть <tt>(a- | Пусть все ключи элементов дерамиды различны. Корнем <tt>T</tt> будет тот элемент <tt>A</tt> или <tt>B</tt>, приоритет которого является максимальным. Нетрудно заметить, что таковым элементом может быть либо <tt>a</tt>, либо <tt>b</tt>. Пусть <tt>(a->p > b->p)</tt>, тогда <tt>a</tt> является корнем результата. Все добавляемые к <tt>A</tt> элементы <tt>B</tt> имеют ключи, большие <tt>a->k</tt>, поэтому они все будут помещены в поддерево <tt>a->r</tt>. Таким образом, мы перешли от задачи объединения <tt>A</tt> и <tt>B</tt> к задаче объединения <tt>a->r</tt> и <tt>B</tt>; налицо рекурсивный характер реализации слияния (симметричный случай рассматривается аналогично). Базой рекурсии является случай, когда хотя бы одна из объединяемых дерамид является пустой. | ||
=== Разрезание | === Разрезание декартова дерева (split) === | ||
Пусть дана дерамида <tt>T</tt> (с корнем <tt>t</tt>) и некоторое число <tt>k</tt>. Требуется составить две дерамиды: <tt>A</tt>, содержащую те элементы <tt>T</tt>, ключи которых меньше <tt>k</tt>, и <tt>B</tt>, содержащую все остальные элементы <tt>T</tt>. Функция должна возвращать два значения; в рассмотренной реализации они передаются через параметры, а возвращаемым типом является <tt>void</tt>. | |||
Пусть дана дерамида <tt>T</tt> (с корнем <tt>t</tt>) и некоторое число <tt>k</tt>. Требуется составить две дерамиды: <tt>A</tt>, содержащую те элементы <tt>T</tt>, ключи которых | |||
void split(TreapNode *t, int k, TreapNode *&a, TreapNode *&b) { | void split(TreapNode *t, int k, TreapNode *&a, TreapNode *&b) { | ||
if (!t) | if (!t) | ||
a = b = NULL; | a = b = NULL; | ||
else if (t->k < | else if (t->k < k) { | ||
split(t->r, k, t->r, b); | split(t->r, k, t->r, b); | ||
a = t; | a = t; | ||
| Строка 69: | Строка 92: | ||
} | } | ||
Если <tt>(t- | Если <tt>(t->k < k)</tt>, то <tt>t</tt> станет элементом <tt>A</tt>, иначе — элементом <tt>B</tt>. Пусть <tt>t</tt> становится частью <tt>A</tt> (нетрудно заметить, что <tt>t</tt> станет корнем <tt>A</tt>), тогда все элементы поддерева <tt>t->l</tt> также становятся частью <tt>A</tt>, так как их ключи меньше <tt>t->k</tt>, а следовательно, меньше <tt>k</tt>. Ситуация с поддеревом <tt>t->r</tt> сложнее: оно может содержать как элементы, ключи которых меньше <tt>k</tt>, так и элементы, ключи которых не меньше <tt>k</tt>. Поступим следующим образом: рекурсивно разрежем <tt>t->r</tt> по <tt>k</tt>, при этом получатся две дерамиды <tt>A'</tt> и <tt>B'</tt>. Дерамиду <tt>A'</tt> нужно оставить на месте <tt>t->r</tt>, тогда <tt>T</tt> будет содержать только элементы, ключи которых меньше <tt>k</tt>. <tt>B'</tt> содержит только элементы с ключами, не меньшими <tt>k</tt>. Таким образом, результатами операции разрезания являются <tt>T</tt> и <tt>B'</tt>. Симметричный случай рассматривается аналогично. Можно видеть, что операция разрезания также реализуется рекурсивно; базой рекурсии является случай, когда <tt>T</tt> пуста. | ||
== Реализация операций двоичного дерева поиска == | |||
Как будет показано ниже, на базе дерамиды очень просто реализуются все основные операции двоичного дерева поиска. При этом, приведённое ранее утверждение о том, что высота дерамиды со случайными приоритетами имеет порядок O(logN), позволяет сделать вывод, что асимптотика основных операций двоичного дерева поиска также не превышает O(logN). Из этого следует, что декартовы деревья можно рассматривать как балансирующиеся двоичные деревья поиска, имеющие достаточно простую реализацию. | |||
Будем считать, что указатель <tt>TreapNode *t</tt> ссылается на корень дерамиды. | |||
=== Вставка элемента === | |||
Пусть в декартово дерево <tt>T</tt> нужно добавить новый элемент с ключом <tt>key</tt> и значением <tt>value</tt>. Этот элемент можно рассмотреть как полноценную дерамиду <tt>Tn</tt> (имеющую только один узел). Следовательно, можно произвести слияние исходной дерамиды с добавляемой. Однако для этого нужно обеспечить выполнение предварительного условия (все ключи в первой дерамиде должны быть не больше любого из ключей во второй дерамиде). Поэтому сначала разрежем <tt>T</tt> на две части: <tt>T1</tt>, содержащую ключи, меньшие <tt>key</tt>, и <tt>T2</tt>, содержащую все остальные ключи. Теперь можно произвести два слияния, после чего элемент будет успешно добавлен в декартово дерево <tt>T</tt>. | |||
void insert(int key, int value) { | |||
TreapNode *tn = new TreapNode(key, value), *t1, *t2; | |||
split(t, key, t1, t2); | |||
t = merge(t1, tn); | |||
t = merge(t, t2); | |||
} | |||
=== Удаление элемента === | |||
Пусть требуется исключить из дерамиды <tt>T</tt> все элементы, ключи которых равны <tt>key</tt>. Разрежем <tt>T</tt> на дерамиды <tt>T1</tt> и <tt>T2</tt> по ключу <tt>key</tt>. Тогда все элементы <tt>T1</tt> имеют ключи, меньшие <tt>key</tt>. Разрежем <tt>T2</tt> по ключу <tt>(key + 1)</tt>: правая получившаяся часть (<tt>T3</tt>) содержит элементы, ключи которых больше <tt>key</tt>, а в <tt>T2</tt> останутся только элементы с ключами, равными <tt>key</tt>. Таким образом, после объединения <tt>T1</tt> и <tt>T3</tt> мы получим декартово дерево, не содержащее элементов с ключами <tt>key</tt>. | |||
Если требуется освободить память, занимаемую исключаемыми элементами, то можно воспользоваться простой рекурсивной процедурой, приведённой справа. | |||
{| width="100%" | |||
| width="50%" | | |||
void remove(int key) { | |||
TreapNode *t1, *t2, *t3; | |||
split(t, key, t1, t2); | |||
split(t2, key + 1, t2, t3); | |||
t = merge(t1, t3); | |||
dispose(t2); | |||
} | |||
| width="10px" | | |||
| width="50%" | | |||
void dispose(TreapNode *n) { | |||
if (n == NULL) | |||
return; | |||
dispose(n->l); | |||
dispose(n->r); | |||
delete n; | |||
} | |||
|} | |||
=== Поиск элемента === | |||
С учётом того, что декартово дерево по ключам продолжает оставаться двоичным деревом поиска (в том случае, когда ключи всех элементов различны), операция отыскания элемента с заданным ключом абсолютно не отличается от таковой для обычного двоичного дерева поиска. | |||
С другой стороны, рассмотренный выше подход к работе с дерамидой с помощью операций <tt>merge()</tt> и <tt>split()</tt> может быть применён и здесь. Часть дерамиды, которая может содержать искомый элемент, выделяется с помощью двух разрезаний; после определения ответа исходную дерамиду требуется восстановить («собрать» обратно). Следует отметить, что в дальнейшем (с введением групповых запросов и групповых модификаций) данный подход оказывается более предпочтительным. | |||
Показанная ниже функция возвращает значение элемента, имеющего указанный ключ. Если таких элементов нет, то возвращается значение <tt>0</tt>. | |||
int find(int key) { | |||
int res = 0; | |||
TreapNode *t1, *t2, *t3; | |||
split(t, key, t1, t2); | |||
split(t2, key + 1, t2, t3); | |||
if (t2 != NULL) | |||
res = t2->v; | |||
t1 = merge(t1, t2); | |||
t = merge(t1, t3); | |||
return res; | |||
} | |||
== Реализация групповых запросов == | |||
Декартовы деревья достаточно просто модифицируются для работы с групповыми запросами на элементах: определению суммы, произведения, подсчёту количества, выявлению максимума и т. п. В качестве примера рассмотрим реализацию запросов количества элементов и суммы их значений. | |||
=== Запросы на всём дереве === | |||
Пусть требуется вычислять сумму значений всех элементов, хранящихся в дерамиде, а также определять количество элементов. | |||
Модифицируем структуру <tt>TreapNode</tt>: добавим поля <tt>cnt</tt> и <tt>sum</tt>, которые будут хранить соответственно количество и сумму значений элементов, расположенных в поддереве, корнем которого является текущий элемент. Очевидно, что в конструкторе <tt>TreapNode</tt> поле <tt>sum</tt> следует проинициализировать значением элемента, а поле <tt>cnt</tt> — единицей. | |||
Также определим несколько вспомогательных процедур. Одна из них — процедура <tt>update()</tt>, которая будет пересчитывать значения <tt>sum</tt> и <tt>cnt</tt> у текущего элемента в предположении, что у его потомков они посчитаны правильно. | |||
{| width="100%" | |||
| width="50%" | | |||
struct TreapNode { | |||
int k, p, v; | |||
'''int sum, cnt;''' | |||
TreapNode *l, *r; | |||
TreapNode(int key, int value) { | |||
k = key; | |||
v = value; | |||
p = rand(); | |||
l = r = NULL; | |||
'''sum = value;''' | |||
'''cnt = 1;''' | |||
} | |||
}; | |||
| width="10px" | | |||
| width="50%" | | |||
int getSum(TreapNode *n) { | |||
return n != NULL ? n->sum : 0; | |||
} | |||
int getCnt(TreapNode *n) { | |||
return n != NULL ? n->cnt : 0; | |||
} | |||
void update(TreapNode *n) { | |||
if (n == NULL) return; | |||
n->sum = v + getSum(n->l) + getSum(n->r); | |||
n->cnt = 1 + getCnt(n->l) + getCnt(n->r); | |||
} | |||
|} | |||
Далее необходимо модифицировать операции <tt>merge()</tt> и <tt>split()</tt> таким образом, чтобы возвращаемые ими результаты имели корректные значения <tt>sum</tt> и <tt>cnt</tt>. Для этого нужно вставить вызовы функции <tt>update()</tt> для каждого возвращаемого значения. Обе процедуры являются рекурсивными, и если внутренние вызовы правильно пересчитывают <tt>sum</tt> и <tt>cnt</tt>, то и текущий вызов обновит их нужным образом. Достаточно легко показать, что базовые случаи (для <tt>merge()</tt> — когда <tt>a</tt> или <tt>b</tt> равно <tt>NULL</tt>, для <tt>split()</tt> — когда <tt>t</tt> равно <tt>NULL</tt>) правильно обрабатываются операцией <tt>update()</tt>, из чего по индукции следует общая корректность обновления. | |||
{| width="100%" | |||
| width="50%" | | |||
TreapNode *merge(TreapNode *a, TreapNode *b) { | |||
if (!a || !b) | |||
return a ? a : b; | |||
if (a->p > b->p) { | |||
a->r = merge(a->r, b); | |||
'''update(a);''' | |||
return a; | |||
} else { | |||
b->l = merge(a, b->l); | |||
'''update(b);''' | |||
return b; | |||
} | |||
} | |||
| width="10px" | | |||
| width="50%" | | |||
void split(TreapNode *t, int k, | |||
TreapNode *&a, TreapNode *&b) { | |||
if (!t) | |||
a = b = NULL; | |||
else if (t->k < k) { | |||
split(t->r, k, t->r, b); | |||
a = t; | |||
} else { | |||
split(t->l, k, a, t->l); | |||
b = t; | |||
} | |||
'''update(a); update(b);''' | |||
} | |||
|} | |||
Теперь, если нужно получить сумму значений или количество элементов в дерамиде, достаточно проверить соответствующее поле у её корня. | |||
=== Запросы на отрезках === | |||
Пусть теперь требуется определять сумму или количество только для элементов, ключи которых принадлежат некоторому отрезку [<tt>k1</tt>; <tt>k2</tt>]. Выделить в дерамиде составляющую, содержащую все элементы с указанными ключами, можно с помощью двух разрезаний (как при поиске или удалении элемента), а определение интересующего значения для всей дерамиды рассмотрено в предыдущем пункте. | |||
Руководствуясь этими рассуждениями, можно привести простую реализацию запроса на подотрезках дерамиды. | |||
int rangeSum(int k1, int k2) { | |||
TreapNode *t1, *t2, *t3; | |||
split(t, k1, t1, t2); | |||
split(t2, k2 + 1, t2, t3); | |||
int s = getSum(t2); | |||
t1 = merge(t1, t2); | |||
t = merge(t1, t3); | |||
return s; | |||
} | |||
== Реализация групповых модификаций == | |||
Декартово дерево также позволяет производить групповую модификацию элементов (умножение на число, замена заданным значением, установка каких-либо свойств и т. д.), в том числе на заданном отрезке. В качестве примера рассмотрим реализацию добавления некоторой величины к значениям хранящихся в дерамиде элементов. | |||
=== Модификации на всём дереве === | |||
Пусть требуется эффективная реализация одновременного добавления некоторой величины к значениям всех элементов дерева. | |||
Добавим в структуру <tt>TreapNode</tt> поле <tt>add</tt>, которое будет хранить число, добавляемое к значениям элементов, расположенных в поддереве, корнем которого является текущий элемент. В конструкторе это поле инициализируется нулём. | |||
Таким образом, теперь фактическим значением, хранящимся в корне дерамиды <tt>T</tt>, является не <tt>t->v</tt>, а <tt>(t->v + t->add)</tt>. Изменяется и сумма значений в дерамиде: если величина <tt>t->sum</tt> определена верно, то фактическое значение суммы будет равно <tt>(t->sum + t->add * t->cnt)</tt>. | |||
{| width="100%" | |||
| width="50%" | | |||
struct TreapNode { | |||
int k, p, v; | |||
int sum, cnt, '''add'''; | |||
TreapNode *l, *r; | |||
TreapNode(int key, int value) { | |||
k = key; | |||
v = value; | |||
p = rand(); | |||
l = r = NULL; | |||
sum = value; | |||
cnt = 1; | |||
'''add = 0;''' | |||
} | |||
}; | |||
| width="10px" | | |||
| width="50%" | | |||
int getSum(TreapNode *n) { | |||
return n != NULL ? n->sum '''+ n->add * n->cnt''' : 0; | |||
} | |||
void down(TreapNode *n) { | |||
if (n == NULL) | |||
return; | |||
n->v += n->add; | |||
if (n->l != NULL) | |||
n->l->add += n->add; | |||
if (n->r != NULL) | |||
n->r->add += n->add; | |||
n->add = 0; | |||
} | |||
|} | |||
Рекурсивные операции <tt>split()</tt> и <tt>merge()</tt>, изменяющие декартово дерево, работают в предположении, что переданные им в качестве параметров дерамиды являются корректными. После добавления поля <tt>add</tt> корректность может нарушиться: например, если <tt>t->add</tt> равно 10, а <tt>t->l->add</tt> равно 0, по после отделения <tt>t->l</tt> от <tt>t</tt> информация о том, что всем элементам <tt>t->l</tt> нужно добавить 10, будет утрачена. Поэтому перед выполнением операций <tt>split()</tt> и <tt>merge()</tt> нужно «передавать» значение <tt>add</tt> потомкам. Это действие удобно выполнять с помощью отдельной процедуры <tt>down()</tt>, код которой приведён выше. | |||
{| width="100%" | |||
| width="50%" | | |||
TreapNode *merge(TreapNode *a, TreapNode *b) { | |||
if (!a || !b) | |||
return a ? a : b; | |||
if (a->p > b->p) { | |||
'''down(a);''' | |||
a->r = merge(a->r, b); | |||
update(a); | |||
return a; | |||
} else { | |||
'''down(b);''' | |||
b->l = merge(a, b->l); | |||
update(b); | |||
return b; | |||
} | |||
} | |||
| width="10px" | | |||
| width="50%" | | |||
void split(TreapNode *t, int k, | |||
TreapNode *&a, TreapNode *&b) { | |||
'''down(t);''' | |||
if (!t) | |||
a = b = NULL; | |||
else if (t->k < k) { | |||
split(t->r, k, t->r, b); | |||
a = t; | |||
} else { | |||
split(t->l, k, a, t->l); | |||
b = t; | |||
} | |||
update(a); | |||
update(b); | |||
} | |||
|} | |||
Теперь, если нужно добавить некоторую величину ко всем элементам дерамиды, то следует присвоить эту величину полю <tt>add</tt> у корня. | |||
=== Модификации на отрезках === | |||
Если реализовано добавление заданной величины всем элементам дерамиды, то нетрудно реализовать и добавление только для элементов, ключи которых принадлежат отрезку [<tt>k1</tt>; <tt>k2</tt>]. Логика действий при этом такая же, как и при реализации запросов на отрезках. | |||
void rangeAdd(int k1, int k2, int addVal) { | |||
TreapNode *t1, *t2, *t3; | |||
split(t, k1, t1, t2); | |||
split(t2, k2 + 1, t2, t3); | |||
if (t2 != NULL) | |||
t2->add += addVal; | |||
t1 = merge(t1, t2); | |||
t = merge(t1, t3); | |||
} | |||
== Задачи, решаемые с помощью декартовых деревьев == | |||
Одним из основных преимуществ декартовых деревьев является сравнительная простота реализации, что нередко оказывается важным в условиях соревнования. Как можно видеть, дерамиды имеют достаточно широкий спектр применения: | |||
*Задачи, в которых требуется достаточно сбалансированное дерево поиска (например, эффективная реализация множеств или словарей); | |||
*Широкий класс задач с запросами на диапазонах (RSQ, RMQ и др.), в том числе с обновлениями на отрезках. В отличие от [[Дерево отрезков|деревьев отрезков]], декартовы деревья позволяют выполнять запросы на изменяющихся множествах; | |||
*Поиск порядковых статистик (определение k-го по величине элемента) за O(logN). В этом случае нужно поддерживать поля <tt>cnt</tt>, и далее по этой информации определять, в каком поддереве будет располагаться нужный элемент; | |||
*Решение обратной задачи (определение номера элемента в отсортированной последовательности) за O(logN). Требуется разрезать дерамиду по заданному ключу и определить количество элементов в левой части; | |||
*Декартово дерево служит основой для ещё более мощной структуры данных, именуемой [[Расширения декартова дерева|декартовым деревом по неявному ключу]], которую можно рассматривать как массив, позволяющий производить большое количество различных операций с логарифмическим временем выполнения. | |||
== Ссылки == | |||
Теория: | |||
* [https://www.youtube.com/watch?v=68mMGJl5F8s&list=PLGhUJWLZ8uQ5Ewplzb1ER29p4-kQme5Yr&index=2 Фолунин В. Декартово дерево (плейлист)] | |||
* [http://e-maxx.ru/algo/treap e-maxx.ru — Декартово дерево] | |||
* [http://neerc.ifmo.ru/wiki/index.php?title=%D0%94%D0%B5%D0%BA%D0%B0%D1%80%D1%82%D0%BE%D0%B2%D0%BE_%D0%B4%D0%B5%D1%80%D0%B5%D0%B2%D0%BE neerc.ifmo.ru/wiki — Декартово дерево] | |||
* [http://habrahabr.ru/post/101818/ habrahabr.ru — Декартово дерево: Часть 1. Описание, операции, применения] | |||
* [http://habrahabr.ru/post/102006/ habrahabr.ru — Декартово дерево: Часть 2. Ценная информация в дереве и множественные операции с ней] | |||
* [http://opentrains.mipt.ru/zksh/files/zksh2015/lectures/zksh_cartesian.pdf Иващенко Д., Семенов К. Декартово дерево] | |||
* [http://yadi.sk/i/0iYC_v63hfnyr Фолунин В. Особенности реализации ассоциативных массивов с дублирующимися ключами на декартовых деревьях] | |||
Код: | |||
* [https://github.com/indy256/codelibrary/blob/master/cpp/structures/treap.h github.com/indy256/codelibrary/blob/master/cpp/structures/treap.h] | |||
* [http://github.com/ADJA/algos/blob/master/DataStructures/CartesianTree.cpp Algos — Cartesian tree] | |||
Задачи: | |||
* [http://informatics.mccme.ru/course/view.php?id=18 informatics.mccme.ru — Курс «Структуры данных» — часть 4] | |||
[[Category: | [[Category:Балансирующиеся деревья]] | ||
Текущая версия от 15:08, 24 мая 2023
TLDR
Общие сведения
Вычислительная сложность большинства операций с двоичными деревьями поиска пропорциональна высоте дерева. Высота дерева определяется порядком добавления и удаления его элементов. Дерево, содержащее N элементов, может иметь высоту от ⌈log2N⌉ до N.
Пусть каждый узел двоичного дерева поиска имеет, кроме ключа, дополнительное значение, именуемое приоритетом, и установлено следующее дополнительное ограничение: элементы дерева по своим приоритетам формируют пирамиду, то есть приоритет каждого из узлов не меньше приоритетов его потомков (случай максимальной пирамиды). Тогда, вне зависимости от порядка операций с получившимся деревом, его форма задана однозначно.
Убедиться в справедливости данного утверждения можно следующим образом. Корнем дерева является элемент с наибольшим приоритетом. В левом поддереве располагаются элементы, ключи которых не превышают ключа корня, в правом поддереве — остальные элементы (дерево продолжает оставаться деревом поиска). Рекурсивно рассматривая левое и правое поддеревья (корнями которых также являются их элементы с максимальными приоритетами, и так далее), приходим к выводу, что положение каждого элемента дерева задано однозначно, зависит от пары (ключ — приоритет) и не зависит от порядка добавления элементов в дерево.
Можно показать, что доля двоичных деревьев поиска из N элементов, высота которых не превышает ⌈4log2N⌉, стремится к 100%. Этот факт позволяет применить идею рандомизированного алгоритма: если приоритеты узлов назначаются при добавлении случайным образом, то вероятность того, что получившееся дерево будет иметь высоту, превышающую ⌈4log2N⌉, становится пренебрежимо малой. Таким образом, дерево поиска со случайными приоритетами, элементы которого формируют пирамиду по приоритетам, позволяет выполнять основные операции со сложностью O(logN).
Описанная структура данных называется декартовым деревом (дерамидой, англ. cartesian tree, treap). Если пары (ключ — приоритет) рассматривать как координаты узла на декартовой плоскости, то любое нарисованное таким образом декартово дерево будет планарным (не будет иметь рёберных пересечений).
Интерфейс
Декартовы деревья позволяют реализовать весь интерфейс обычных двоичных деревьев поиска, однако позволяют (с высокой вероятностью) выполнять все операции со сложностью O(logN).
| void | insert(T1 key, T2 value) | — добавление пары (key, value) в декартово дерево; | |
| void | remove(T1 key) | — исключение из дерева всех элементов, ключи которых равны key; | |
| T2 | find(T1 key) | — получение значения, сопоставленного с ключом key. |
Кроме того, на декартовых деревьях достаточно просто реализуются различные выборки и групповые модификации:
| T2 | query(T1 key1, T1 key2) | — запрос некоторой функции (суммы, произведения, максимума и т. п.) для всех элементов, ключи которых принадлежат диапазону [key1; key2]; | |
| void | modify(T1 key1, T1 key2) | — групповая модификация (прибавление некоторой величины, умножение на некоторую величину, установка свойств и т. д.) для всех элементов, ключи которых принадлежат диапазону [key1; key2]. |
Следует отметить, что всё многообразие методов на декартовых деревьях основывается на двух базовых операциях, речь о которых пойдёт ниже — объединении дерамид и разрезании дерамиды по ключу.
Реализация базовых операций
Прежде всего определим тип элемента дерамиды TreapNode. Его полями являются ключ, приоритет и хранимое значение, а также указатели на левого и правого потомков.
struct TreapNode {
int k, p, v;
TreapNode *l, *r;
TreapNode(int key, int value) {
k = key;
v = value;
p = rand();
l = r = NULL;
}
};
Слияние декартовых деревьев (merge)
Пусть даны две дерамиды A (с корнем a) и B (с корнем b), причём все ключи элементов A меньше ключа любого элемента B (или не превышают его, в том случае, когда в дерамиде разрешены элементы с равными ключами). Требуется сформировать новую дерамиду T из элементов A и B и вернуть указатель на её корень.
TreapNode *merge(TreapNode *a, TreapNode *b) {
if (!a || !b)
return a ? a : b;
if (a->p > b->p) {
a->r = merge(a->r, b);
return a;
} else {
b->l = merge(a, b->l);
return b;
}
}
Пусть все ключи элементов дерамиды различны. Корнем T будет тот элемент A или B, приоритет которого является максимальным. Нетрудно заметить, что таковым элементом может быть либо a, либо b. Пусть (a->p > b->p), тогда a является корнем результата. Все добавляемые к A элементы B имеют ключи, большие a->k, поэтому они все будут помещены в поддерево a->r. Таким образом, мы перешли от задачи объединения A и B к задаче объединения a->r и B; налицо рекурсивный характер реализации слияния (симметричный случай рассматривается аналогично). Базой рекурсии является случай, когда хотя бы одна из объединяемых дерамид является пустой.
Разрезание декартова дерева (split)
Пусть дана дерамида T (с корнем t) и некоторое число k. Требуется составить две дерамиды: A, содержащую те элементы T, ключи которых меньше k, и B, содержащую все остальные элементы T. Функция должна возвращать два значения; в рассмотренной реализации они передаются через параметры, а возвращаемым типом является void.
void split(TreapNode *t, int k, TreapNode *&a, TreapNode *&b) {
if (!t)
a = b = NULL;
else if (t->k < k) {
split(t->r, k, t->r, b);
a = t;
} else {
split(t->l, k, a, t->l);
b = t;
}
}
Если (t->k < k), то t станет элементом A, иначе — элементом B. Пусть t становится частью A (нетрудно заметить, что t станет корнем A), тогда все элементы поддерева t->l также становятся частью A, так как их ключи меньше t->k, а следовательно, меньше k. Ситуация с поддеревом t->r сложнее: оно может содержать как элементы, ключи которых меньше k, так и элементы, ключи которых не меньше k. Поступим следующим образом: рекурсивно разрежем t->r по k, при этом получатся две дерамиды A' и B'. Дерамиду A' нужно оставить на месте t->r, тогда T будет содержать только элементы, ключи которых меньше k. B' содержит только элементы с ключами, не меньшими k. Таким образом, результатами операции разрезания являются T и B'. Симметричный случай рассматривается аналогично. Можно видеть, что операция разрезания также реализуется рекурсивно; базой рекурсии является случай, когда T пуста.
Реализация операций двоичного дерева поиска
Как будет показано ниже, на базе дерамиды очень просто реализуются все основные операции двоичного дерева поиска. При этом, приведённое ранее утверждение о том, что высота дерамиды со случайными приоритетами имеет порядок O(logN), позволяет сделать вывод, что асимптотика основных операций двоичного дерева поиска также не превышает O(logN). Из этого следует, что декартовы деревья можно рассматривать как балансирующиеся двоичные деревья поиска, имеющие достаточно простую реализацию.
Будем считать, что указатель TreapNode *t ссылается на корень дерамиды.
Вставка элемента
Пусть в декартово дерево T нужно добавить новый элемент с ключом key и значением value. Этот элемент можно рассмотреть как полноценную дерамиду Tn (имеющую только один узел). Следовательно, можно произвести слияние исходной дерамиды с добавляемой. Однако для этого нужно обеспечить выполнение предварительного условия (все ключи в первой дерамиде должны быть не больше любого из ключей во второй дерамиде). Поэтому сначала разрежем T на две части: T1, содержащую ключи, меньшие key, и T2, содержащую все остальные ключи. Теперь можно произвести два слияния, после чего элемент будет успешно добавлен в декартово дерево T.
void insert(int key, int value) {
TreapNode *tn = new TreapNode(key, value), *t1, *t2;
split(t, key, t1, t2);
t = merge(t1, tn);
t = merge(t, t2);
}
Удаление элемента
Пусть требуется исключить из дерамиды T все элементы, ключи которых равны key. Разрежем T на дерамиды T1 и T2 по ключу key. Тогда все элементы T1 имеют ключи, меньшие key. Разрежем T2 по ключу (key + 1): правая получившаяся часть (T3) содержит элементы, ключи которых больше key, а в T2 останутся только элементы с ключами, равными key. Таким образом, после объединения T1 и T3 мы получим декартово дерево, не содержащее элементов с ключами key.
Если требуется освободить память, занимаемую исключаемыми элементами, то можно воспользоваться простой рекурсивной процедурой, приведённой справа.
void remove(int key) {
TreapNode *t1, *t2, *t3;
split(t, key, t1, t2);
split(t2, key + 1, t2, t3);
t = merge(t1, t3);
dispose(t2);
}
|
void dispose(TreapNode *n) {
if (n == NULL)
return;
dispose(n->l);
dispose(n->r);
delete n;
}
|
Поиск элемента
С учётом того, что декартово дерево по ключам продолжает оставаться двоичным деревом поиска (в том случае, когда ключи всех элементов различны), операция отыскания элемента с заданным ключом абсолютно не отличается от таковой для обычного двоичного дерева поиска.
С другой стороны, рассмотренный выше подход к работе с дерамидой с помощью операций merge() и split() может быть применён и здесь. Часть дерамиды, которая может содержать искомый элемент, выделяется с помощью двух разрезаний; после определения ответа исходную дерамиду требуется восстановить («собрать» обратно). Следует отметить, что в дальнейшем (с введением групповых запросов и групповых модификаций) данный подход оказывается более предпочтительным.
Показанная ниже функция возвращает значение элемента, имеющего указанный ключ. Если таких элементов нет, то возвращается значение 0.
int find(int key) {
int res = 0;
TreapNode *t1, *t2, *t3;
split(t, key, t1, t2);
split(t2, key + 1, t2, t3);
if (t2 != NULL)
res = t2->v;
t1 = merge(t1, t2);
t = merge(t1, t3);
return res;
}
Реализация групповых запросов
Декартовы деревья достаточно просто модифицируются для работы с групповыми запросами на элементах: определению суммы, произведения, подсчёту количества, выявлению максимума и т. п. В качестве примера рассмотрим реализацию запросов количества элементов и суммы их значений.
Запросы на всём дереве
Пусть требуется вычислять сумму значений всех элементов, хранящихся в дерамиде, а также определять количество элементов.
Модифицируем структуру TreapNode: добавим поля cnt и sum, которые будут хранить соответственно количество и сумму значений элементов, расположенных в поддереве, корнем которого является текущий элемент. Очевидно, что в конструкторе TreapNode поле sum следует проинициализировать значением элемента, а поле cnt — единицей.
Также определим несколько вспомогательных процедур. Одна из них — процедура update(), которая будет пересчитывать значения sum и cnt у текущего элемента в предположении, что у его потомков они посчитаны правильно.
struct TreapNode {
int k, p, v;
int sum, cnt;
TreapNode *l, *r;
TreapNode(int key, int value) {
k = key;
v = value;
p = rand();
l = r = NULL;
sum = value;
cnt = 1;
}
};
|
int getSum(TreapNode *n) {
return n != NULL ? n->sum : 0;
}
int getCnt(TreapNode *n) {
return n != NULL ? n->cnt : 0;
}
void update(TreapNode *n) {
if (n == NULL) return;
n->sum = v + getSum(n->l) + getSum(n->r);
n->cnt = 1 + getCnt(n->l) + getCnt(n->r);
}
|
Далее необходимо модифицировать операции merge() и split() таким образом, чтобы возвращаемые ими результаты имели корректные значения sum и cnt. Для этого нужно вставить вызовы функции update() для каждого возвращаемого значения. Обе процедуры являются рекурсивными, и если внутренние вызовы правильно пересчитывают sum и cnt, то и текущий вызов обновит их нужным образом. Достаточно легко показать, что базовые случаи (для merge() — когда a или b равно NULL, для split() — когда t равно NULL) правильно обрабатываются операцией update(), из чего по индукции следует общая корректность обновления.
TreapNode *merge(TreapNode *a, TreapNode *b) {
if (!a || !b)
return a ? a : b;
if (a->p > b->p) {
a->r = merge(a->r, b);
update(a);
return a;
} else {
b->l = merge(a, b->l);
update(b);
return b;
}
}
|
void split(TreapNode *t, int k,
TreapNode *&a, TreapNode *&b) {
if (!t)
a = b = NULL;
else if (t->k < k) {
split(t->r, k, t->r, b);
a = t;
} else {
split(t->l, k, a, t->l);
b = t;
}
update(a); update(b);
}
|
Теперь, если нужно получить сумму значений или количество элементов в дерамиде, достаточно проверить соответствующее поле у её корня.
Запросы на отрезках
Пусть теперь требуется определять сумму или количество только для элементов, ключи которых принадлежат некоторому отрезку [k1; k2]. Выделить в дерамиде составляющую, содержащую все элементы с указанными ключами, можно с помощью двух разрезаний (как при поиске или удалении элемента), а определение интересующего значения для всей дерамиды рассмотрено в предыдущем пункте.
Руководствуясь этими рассуждениями, можно привести простую реализацию запроса на подотрезках дерамиды.
int rangeSum(int k1, int k2) {
TreapNode *t1, *t2, *t3;
split(t, k1, t1, t2);
split(t2, k2 + 1, t2, t3);
int s = getSum(t2);
t1 = merge(t1, t2);
t = merge(t1, t3);
return s;
}
Реализация групповых модификаций
Декартово дерево также позволяет производить групповую модификацию элементов (умножение на число, замена заданным значением, установка каких-либо свойств и т. д.), в том числе на заданном отрезке. В качестве примера рассмотрим реализацию добавления некоторой величины к значениям хранящихся в дерамиде элементов.
Модификации на всём дереве
Пусть требуется эффективная реализация одновременного добавления некоторой величины к значениям всех элементов дерева.
Добавим в структуру TreapNode поле add, которое будет хранить число, добавляемое к значениям элементов, расположенных в поддереве, корнем которого является текущий элемент. В конструкторе это поле инициализируется нулём.
Таким образом, теперь фактическим значением, хранящимся в корне дерамиды T, является не t->v, а (t->v + t->add). Изменяется и сумма значений в дерамиде: если величина t->sum определена верно, то фактическое значение суммы будет равно (t->sum + t->add * t->cnt).
struct TreapNode {
int k, p, v;
int sum, cnt, add;
TreapNode *l, *r;
TreapNode(int key, int value) {
k = key;
v = value;
p = rand();
l = r = NULL;
sum = value;
cnt = 1;
add = 0;
}
};
|
int getSum(TreapNode *n) {
return n != NULL ? n->sum + n->add * n->cnt : 0;
}
void down(TreapNode *n) {
if (n == NULL)
return;
n->v += n->add;
if (n->l != NULL)
n->l->add += n->add;
if (n->r != NULL)
n->r->add += n->add;
n->add = 0;
}
|
Рекурсивные операции split() и merge(), изменяющие декартово дерево, работают в предположении, что переданные им в качестве параметров дерамиды являются корректными. После добавления поля add корректность может нарушиться: например, если t->add равно 10, а t->l->add равно 0, по после отделения t->l от t информация о том, что всем элементам t->l нужно добавить 10, будет утрачена. Поэтому перед выполнением операций split() и merge() нужно «передавать» значение add потомкам. Это действие удобно выполнять с помощью отдельной процедуры down(), код которой приведён выше.
TreapNode *merge(TreapNode *a, TreapNode *b) {
if (!a || !b)
return a ? a : b;
if (a->p > b->p) {
down(a);
a->r = merge(a->r, b);
update(a);
return a;
} else {
down(b);
b->l = merge(a, b->l);
update(b);
return b;
}
}
|
void split(TreapNode *t, int k,
TreapNode *&a, TreapNode *&b) {
down(t);
if (!t)
a = b = NULL;
else if (t->k < k) {
split(t->r, k, t->r, b);
a = t;
} else {
split(t->l, k, a, t->l);
b = t;
}
update(a);
update(b);
}
|
Теперь, если нужно добавить некоторую величину ко всем элементам дерамиды, то следует присвоить эту величину полю add у корня.
Модификации на отрезках
Если реализовано добавление заданной величины всем элементам дерамиды, то нетрудно реализовать и добавление только для элементов, ключи которых принадлежат отрезку [k1; k2]. Логика действий при этом такая же, как и при реализации запросов на отрезках.
void rangeAdd(int k1, int k2, int addVal) {
TreapNode *t1, *t2, *t3;
split(t, k1, t1, t2);
split(t2, k2 + 1, t2, t3);
if (t2 != NULL)
t2->add += addVal;
t1 = merge(t1, t2);
t = merge(t1, t3);
}
Задачи, решаемые с помощью декартовых деревьев
Одним из основных преимуществ декартовых деревьев является сравнительная простота реализации, что нередко оказывается важным в условиях соревнования. Как можно видеть, дерамиды имеют достаточно широкий спектр применения:
- Задачи, в которых требуется достаточно сбалансированное дерево поиска (например, эффективная реализация множеств или словарей);
- Широкий класс задач с запросами на диапазонах (RSQ, RMQ и др.), в том числе с обновлениями на отрезках. В отличие от деревьев отрезков, декартовы деревья позволяют выполнять запросы на изменяющихся множествах;
- Поиск порядковых статистик (определение k-го по величине элемента) за O(logN). В этом случае нужно поддерживать поля cnt, и далее по этой информации определять, в каком поддереве будет располагаться нужный элемент;
- Решение обратной задачи (определение номера элемента в отсортированной последовательности) за O(logN). Требуется разрезать дерамиду по заданному ключу и определить количество элементов в левой части;
- Декартово дерево служит основой для ещё более мощной структуры данных, именуемой декартовым деревом по неявному ключу, которую можно рассматривать как массив, позволяющий производить большое количество различных операций с логарифмическим временем выполнения.
Ссылки
Теория:
- Фолунин В. Декартово дерево (плейлист)
- e-maxx.ru — Декартово дерево
- neerc.ifmo.ru/wiki — Декартово дерево
- habrahabr.ru — Декартово дерево: Часть 1. Описание, операции, применения
- habrahabr.ru — Декартово дерево: Часть 2. Ценная информация в дереве и множественные операции с ней
- Иващенко Д., Семенов К. Декартово дерево
- Фолунин В. Особенности реализации ассоциативных массивов с дублирующимися ключами на декартовых деревьях
Код:
Задачи: