Очередь с приоритетами: различия между версиями
Ctrlalt (обсуждение | вклад) Нет описания правки |
Ctrlalt (обсуждение | вклад) Нет описания правки |
||
| (не показано 49 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
== TLDR == | |||
<youtube width="300" height="180">o1ZDXf7NGN4</youtube> | |||
<youtube width="300" height="180">wArwjbpWFkw</youtube> | |||
== Общие сведения == | == Общие сведения == | ||
Очередь с приоритетами (англ. priority queue) — абстрактный контейнер, похожий на обычную очередь, но имеющий ряд особенностей: | Очередь с приоритетами (англ. priority queue) — абстрактный контейнер, похожий на обычную очередь, но имеющий ряд особенностей: | ||
| Строка 5: | Строка 9: | ||
*Функция извлечения из очереди с приоритетами возвращает тот элемент, приоритет которого является максимальным. | *Функция извлечения из очереди с приоритетами возвращает тот элемент, приоритет которого является максимальным. | ||
Учащийся, выполняющий домашнее задание по нескольким предметам, может вводить различные показатели, определяющие порядок выполнения: от более любимых предметов к менее любимым, от менее сложных к более сложным, и так далее. Пожарная | Учащийся, выполняющий домашнее задание по нескольким предметам, может вводить различные показатели, определяющие порядок выполнения: от более любимых предметов к менее любимым, от менее сложных к более сложным, и так далее. Пожарная бригада планирует выезды сообразно с категорией сложности возгорания. Операционная система компьютера выделяет аппаратные ресурсы в первую очередь приложениям, запущенным с приоритетом реального времени, и лишь затем — остальным приложениям. Эти примеры позволяют пояснить назначение и принципы функционирования очередей с приоритетами. | ||
== Интерфейс == | == Интерфейс == | ||
| Строка 11: | Строка 15: | ||
Интерфейс очереди с приоритетами в целом аналогичен интерфейсу обычной очереди, но в операции добавления появляется второй аргумент, а операция удаления возвращает элемент с наибольшим приоритетом: | Интерфейс очереди с приоритетами в целом аналогичен интерфейсу обычной очереди, но в операции добавления появляется второй аргумент, а операция удаления возвращает элемент с наибольшим приоритетом: | ||
{| | {| class="methodlist" | ||
| | | || void || enqueue(T1 value, T2 priority) || — вставка элемента <tt>value</tt> с приоритетом <tt>priority</tt> в очередь; | ||
|- | |- | ||
| | | || T1 || dequeue() || — извлечение элемента с максимальным приоритетом из очереди; | ||
|- | |- | ||
| | | || bool || isEmpty() || — проверка очереди на отсутствие элементов. | ||
|} | |} | ||
== Демонстрация работы == | == Демонстрация работы == | ||
[[ | * [http://www.cs.usfca.edu/~galles/visualization/Heap.html Data Structure Visualizations — Min Heap] | ||
: В демонстрации показана очередь, в которой наивысший приоритет имеет наименьший элемент. Эта очередь построена на невозрастающей пирамиде (англ. min-oriented heap). | |||
: В статье рассматривается реализация очереди, в которой наивысший приоритет имеет наибольший элемент; соответствующая ей пирамида называется неубывающей (англ. max-oriented). | |||
* [http://visualgo.net/heap.html VisuAlgo — Binary Heap] | |||
== Реализация == | == Реализация == | ||
Очередь с приоритетами, построенная на обычном | Очередь с приоритетами, построенная на обычном массиве или списке, позволяет выполнять вставку за O(1), но поиск и удаление элемента с максимальным приоритетом будут иметь сложность O(N). Существует более быстрая реализация очереди с приоритетами, подразумевающая применение особого способа организации данных, получившего название пирамиды (англ. heap, также используется термин «куча»; не следует путать с динамическим хранилищем данных в памяти, которое также именуется кучей). | ||
=== Определение пирамиды === | |||
Пирамида — это двоичное дерево, для элементов которого выполняется дополнительное условие (называемое ''основным свойством пирамиды''): значение элемента в родительском узле больше (более точно, не меньше) значений во всех узлах-потомках. | |||
Пирамида | [[Файл:heap.png|thumb|right|360px|Пирамида, отображаемая на массив]] | ||
Пирамиду можно построить на массиве, используя соотношения | Пирамиду можно построить на массиве, используя соотношения между индексами ячеек массива для определения связей элементов. На иллюстрации показан пример пирамиды, содержащей 8 элементов, и её отображение на массив. | ||
Если индексация элементов массива начинается с единицы, то непосредственные потомки элемента с индексом <tt>i</tt> будут иметь индексы <tt>(2 * i)</tt> и <tt>(2 * i + 1)</tt>, а родителем будет являться элемент с индексом <tt>(i / 2)</tt>. Так, потомками элемента с индексом 1 будут элементы с индексами 2 и 3, потомками элемента с индексом 2 — элементы с индексами 4 и 5, родителем элемента с индексом 8 будет элемент с индексом 4. | Если индексация элементов массива начинается с единицы, то непосредственные потомки элемента с индексом <tt>i</tt> будут иметь индексы <tt>(2 * i)</tt> и <tt>(2 * i + 1)</tt>, а родителем будет являться элемент с индексом <tt>(i / 2)</tt>. Так, потомками элемента с индексом 1 будут элементы с индексами 2 и 3, потомками элемента с индексом 2 — элементы с индексами 4 и 5, родителем элемента с индексом 8 будет элемент с индексом 4. | ||
Если индексация элементов массива начинается с нуля, то непосредственные потомки элемента с индексом <tt>i</tt> будут иметь индексы <tt>(2 * i + 1)</tt> и <tt>(2 * i + 2)</tt>, а родителем будет являться элемент с индексом <tt>((i | Если индексация элементов массива начинается с нуля, то непосредственные потомки элемента с индексом <tt>i</tt> будут иметь индексы <tt>(2 * i + 1)</tt> и <tt>(2 * i + 2)</tt>, а родителем будет являться элемент с индексом <tt>((i - 1) / 2)</tt>. Так, потомками элемента с индексом 0 будут элементы с индексами 1 и 2, потомками элемента с индексом 1 — элементы с индексами 3 и 4, родителем элемента с индексом 7 будет элемент с индексом 3. | ||
В целях упрощения дальнейшего кода определим вспомогательные функции <tt>parent()</tt>, <tt>leftChild()</tt> и <tt>rightChild()</tt>: | |||
int parent(int i) { | |||
return (i - 1) / 2; | |||
} | |||
int leftChild(int i) { | |||
return 2 * i + 1; | |||
} | |||
int rightChild(int i) { | |||
return 2 * i + 2; | |||
} | |||
Пирамида является почти полным двоичным деревом: только самый нижний уровень может быть не заполнен полностью, и его заполнение происходит строго слева направо. Можно показать, что в N-элементной пирамиде ⌈N/2⌉ последних элементов являются листьями, то есть не имеют потомков. При индексации массива с единицы листья имеют индексы от <tt>(N / 2 + 1)</tt> до <tt>N</tt>, при индексации с нуля — от <tt>(N / 2)</tt> до <tt>(N - 1)</tt>. | Пирамида в данной реализации является почти полным двоичным деревом: только самый нижний уровень может быть не заполнен полностью, и его заполнение происходит строго слева направо. Можно показать, что в N-элементной пирамиде ⌈N/2⌉ последних элементов являются листьями, то есть не имеют потомков. При индексации массива с единицы листья имеют индексы от <tt>(N / 2 + 1)</tt> до <tt>N</tt>, при индексации с нуля — от <tt>(N / 2)</tt> до <tt>(N - 1)</tt>. | ||
''Высотой пирамиды'' называется количество рёбер на самом длинном пути от вершины пирамиды до какого-либо листа. Достаточно легко убедиться, что высота пирамиды из N элементов равна | ''Высотой пирамиды'' называется количество рёбер на самом длинном пути от вершины пирамиды до какого-либо листа. Достаточно легко убедиться, что высота почти полной пирамиды из N элементов равна ⌊log<sub>2</sub>N⌋. | ||
=== Поддержка основного свойства пирамиды === | === Поддержка основного свойства пирамиды === | ||
| Строка 42: | Строка 66: | ||
*Значение элемента больше, чем у его родителя, и поэтому элемент должен занять место выше, чем имеет сейчас; | *Значение элемента больше, чем у его родителя, и поэтому элемент должен занять место выше, чем имеет сейчас; | ||
*Значение элемента меньше, чем у хотя бы одного из его потомков, и поэтому элемент должен занять место ниже, чем имеет сейчас. | *Значение элемента меньше, чем у хотя бы одного из его потомков, и поэтому элемент должен занять место ниже, чем имеет сейчас. | ||
[[Файл:heap_up.gif|thumb|right|360px|Восстановление пирамиды — операция up()]] | |||
Процедура <tt>up()</tt>, которая будет исправлять нарушения первого типа, обменивает заданный элемент с его родителем до тех пор, пока значение элемента не станет меньше значения родителя, либо элемент не окажется на вершине пирамиды. Процедура принимает индекс элемента, который вызывает нарушение основного свойства пирамиды. Приведённый ниже код работает для массива, в котором индексация начинается с нуля. | Процедура <tt>up()</tt>, которая будет исправлять нарушения первого типа, обменивает заданный элемент с его родителем до тех пор, пока значение элемента не станет меньше значения родителя, либо элемент не окажется на вершине пирамиды. Процедура принимает индекс элемента, который вызывает нарушение основного свойства пирамиды. Приведённый ниже код работает для массива, в котором индексация начинается с нуля. | ||
void up(int i) { | void up(int i) { | ||
while (i != 0 && a[i] > a[(i | while (i != 0 && a[i] > a[parent(i)]) { | ||
swap(a[i], a[parent(i)]; | |||
i = parent(i); | |||
i = (i | |||
} | } | ||
} | } | ||
[[Файл:heap_down.gif|thumb|right|360px|Восстановление пирамиды — операция down()]] | |||
Процедура <tt>down()</tt>, исправляющая нарушения второго типа, обменивает заданный элемент с максимальным из его потомков до тех пор, пока значение элемента не станет больше значений потомков, либо элемент не окажется листом. Обмен происходит с максимальным из потомков, так как только в этом случае основное свойство пирамиды гарантированно поддерживается после обмена. Как и в предыдущем случае, процедура принимает индекс неверно расположенного элемента в массиве, а индексация элементов начинается с нуля. Общее количество элементов в очереди равно <tt>size</tt>. | Процедура <tt>down()</tt>, исправляющая нарушения второго типа, обменивает заданный элемент с максимальным из его потомков до тех пор, пока значение элемента не станет больше значений потомков, либо элемент не окажется листом. Обмен происходит с максимальным из потомков, так как только в этом случае основное свойство пирамиды гарантированно поддерживается после обмена. Как и в предыдущем случае, процедура принимает индекс неверно расположенного элемента в массиве, а индексация элементов начинается с нуля. Общее количество элементов в очереди равно <tt>size</tt>. | ||
| Строка 58: | Строка 84: | ||
void down(int i) { | void down(int i) { | ||
while (i < size / 2) { | while (i < size / 2) { | ||
int maxI = leftChild(i); | |||
if (rightChild(i) < size && a[rightChild(i)] > a[leftChild(i)]) | |||
maxI = rightChild(i); | |||
if (a[i] >= a[maxI]) | if (a[i] >= a[maxI]) | ||
return; | return; | ||
swap(a[i], a[maxI]); | |||
i = maxI; | i = maxI; | ||
} | } | ||
| Строка 100: | Строка 124: | ||
if (size == 0) | if (size == 0) | ||
/* обработка ошибки - нет элементов для извлечения */ | /* обработка ошибки - нет элементов для извлечения */ | ||
a[0] | swap(a[0], a[--size]); | ||
down(0); | down(0); | ||
return a[size]; | return a[size].val; | ||
} | } | ||
---- | ---- | ||
Ниже приведён полный код реализации очереди с приоритетами. | Ниже приведён полный код реализации очереди с приоритетами. Переполнение и попытка извлечения из пустой очереди выявляются с помощью конструкции [http://www.cplusplus.com/reference/cassert/assert/ assert] (заголовочный файл <tt><assert.h></tt> либо <tt><cassert></tt>). | ||
class PriorityQueue { | class PriorityQueue { | ||
| Строка 123: | Строка 147: | ||
void up(int i) { | void up(int i) { | ||
while (i != 0 && a[i].priority > a[(i | while (i != 0 && a[i].priority > a[(i - 1) / 2].priority) { | ||
swap(a[i], a[(i - 1) / 2]); | |||
i = (i - 1) / 2; | |||
i = (i | |||
} | } | ||
} | } | ||
| Строка 138: | Строка 160: | ||
if (a[i].priority >= a[maxI].priority) | if (a[i].priority >= a[maxI].priority) | ||
return; | return; | ||
swap(a[i], a[maxI]); | |||
i = maxI; | i = maxI; | ||
} | } | ||
| Строка 152: | Строка 172: | ||
void enqueue(int value, int priority) { | void enqueue(int value, int priority) { | ||
assert(size + 1 < MAX_SIZE); | |||
a[size++] = Elem(value, priority); | a[size++] = Elem(value, priority); | ||
up(size - 1); | up(size - 1); | ||
| Строка 159: | Строка 178: | ||
int dequeue() { | int dequeue() { | ||
assert(size > 0); | |||
swap(a[0], a[--size]); | |||
a[0] | |||
down(0); | down(0); | ||
return a[size]; | return a[size].val; | ||
} | } | ||
| Строка 173: | Строка 191: | ||
== Очередь с приоритетами в STL == | == Очередь с приоритетами в STL == | ||
В стандартной библиотеке шаблонов C++ присутствует шаблон <tt>priority_queue<T></tt>. Для возможности его использования требуется подключить заголовочный файл <tt><queue></tt> и пространство имён <tt>std</tt>. | В стандартной библиотеке шаблонов C++ присутствует шаблон [http://www.cplusplus.com/reference/queue/priority_queue/ <tt>priority_queue<T></tt>]. Для возможности его использования требуется подключить заголовочный файл <tt><queue></tt> и пространство имён <tt>std</tt>. | ||
#include <iostream> | #include <iostream> | ||
| Строка 194: | Строка 212: | ||
Набор методов для очереди с приоритетами в STL почти полностью аналогичен таковому для обычной очереди: | Набор методов для очереди с приоритетами в STL почти полностью аналогичен таковому для обычной очереди: | ||
{| | {| class="methodlist" | ||
| | | || || priority_queue<T>() || — конструктор; | ||
|- | |- | ||
| | | || void || push(const T& x) || — добавление элемента в очередь. Приоритет элемента определяется его значением; | ||
|- | |- | ||
| | | || void || pop() || — удаление элемента с максимальным приоритетом. Обратите внимание на то, что значение удаляемого элемента не возвращается; | ||
|- | |- | ||
| | | || T& || top() || — получение значения элемента с максимальным приоритетом. Этот метод не производит удаление элемента; | ||
|- | |- | ||
| | | || bool || empty() || — проверка очереди с приоритетами на пустоту; | ||
|- | |- | ||
| | | || size_t || size() || — получение количества элементов в очереди с приоритетами. Метод возвращает беззнаковое целое число. | ||
|} | |} | ||
Очередь с приоритетами в STL создаётся на базе шаблона последовательного контейнера с произвольным доступом (<tt>vector</tt> или <tt>deque</tt>), и для поддержания внутренней структуры она использует процедуры работы с пирамидами, определённые в заголовочном файле <tt><algorithm></tt>. Каждая из них принимает пару итераторов произвольного доступа <tt>It</tt>, указывающих диапазон элементов (как правило, это <tt>begin()</tt> и <tt>end()</tt>, покрывающие все элементы в контейнере). По умолчанию для сравнения во всех процедурах используется оператор <tt><</tt>; собственный функциональный объект можно передать третьим параметром. | Очередь с приоритетами в STL создаётся на базе шаблона последовательного контейнера с произвольным доступом (<tt>vector</tt> или <tt>deque</tt>), и для поддержания внутренней структуры она использует процедуры работы с пирамидами, определённые в заголовочном файле <tt><algorithm></tt>. Каждая из них принимает пару итераторов произвольного доступа <tt>It</tt>, указывающих диапазон элементов (как правило, это <tt>begin()</tt> и <tt>end()</tt>, покрывающие все элементы в контейнере). По умолчанию для сравнения во всех процедурах используется оператор <tt><</tt>; собственный функциональный объект можно передать третьим параметром. | ||
{| | {| class="methodlist" | ||
| | | || void || make_heap(It first, It last) || — создание пирамиды из диапазона элементов [<tt>first</tt>, <tt>last</tt>); | ||
|- | |- | ||
| | | || void || push_heap(It first, It last) || — добавление элемента, находящегося перед <tt>last</tt>, в пирамиду [<tt>first</tt>, <tt>last-1</tt>), так что весь диапазон [<tt>first</tt>, <tt>last</tt>) становится пирамидой; | ||
|- | |- | ||
| | | || void || pop_heap(It first, It last) || — перемещение элемента с максимальным приоритетом (на который изначально указывает <tt>first</tt>) в конец и формирование пирамиды в диапазоне [<tt>first</tt>, <tt>last-1</tt>) из оставшихся элементов; | ||
|- | |- | ||
| | | || void || sort_heap(It first, It last) || — преобразование пирамиды [<tt>first</tt>, <tt>last</tt>) в упорядоченный интервал. После вызова процедуры диапазон перестаёт быть пирамидой. | ||
|} | |} | ||
| Строка 225: | Строка 243: | ||
Вместо последовательного поиска наименьшего элемента можно использовать пирамиду, позволяющую на каждом шаге извлекать минимальный элемент за O(1) и восстанавливаться за O(logN), что даст итоговую сложность O(NlogN). Чтобы не перемещать саму пирамиду, на каждом шаге можно извлекать максимальный элемент и перемещать его в конец. Построить пирамиду на непустом данном массиве можно двумя способами: | Вместо последовательного поиска наименьшего элемента можно использовать пирамиду, позволяющую на каждом шаге извлекать минимальный элемент за O(1) и восстанавливаться за O(logN), что даст итоговую сложность O(NlogN). Чтобы не перемещать саму пирамиду, на каждом шаге можно извлекать максимальный элемент и перемещать его в конец. Построить пирамиду на непустом данном массиве можно двумя способами: | ||
*Проходя от начала массива до конца, последовательно выполнить для каждого элемента операцию <tt>up()</tt> (что в целом аналогично построению очереди с приоритетами за счёт выполнения операции enqueue() для каждого элемента массива). Сложность O(NlogN); | *Проходя от начала массива до конца, последовательно выполнить для каждого элемента операцию <tt>up()</tt> (что в целом аналогично построению очереди с приоритетами за счёт выполнения операции <tt>enqueue()</tt> для каждого элемента массива). Сложность O(NlogN); | ||
*Построить пирамиду «снизу вверх», проходя от конца массива до начала и вызывая процедуру <tt>down()</tt> для всех элементов. Вызов down() для листьев не предусматривает никаких действий, поэтому можно начинать цикл с <tt>(size / 2 - 1)</tt>. В нескольких источниках, в том числе в книге Т. Кормена «Алгоритмы: построение и анализ», показано, что сложность данного метода снижается до O(N). | *Построить пирамиду «снизу вверх», проходя от конца массива до начала и вызывая процедуру <tt>down()</tt> для всех элементов. Вызов <tt>down()</tt> для листьев не предусматривает никаких действий, поэтому можно начинать цикл с <tt>(size / 2 - 1)</tt>. В нескольких источниках, в том числе в книге Т. Кормена «Алгоритмы: построение и анализ», показано, что сложность данного метода снижается до O(N). | ||
Пусть функция <tt>down()</tt> использует значения <tt>a[]</tt> и <tt>size</tt>, переданные ей через параметры. Тогда код пирамидальной сортировки имеет следующий вид: | |||
void heapsort(int a[], int size) { | void heapsort(int a[], int size) { | ||
for (int i = size / 2 - 1; i >= 0; i--) | for (int i = size / 2 - 1; i >= 0; i--) | ||
down(i); | down(a, size, i); | ||
for (int i = 0; i < | for (int i = 0; i < size; i++) { | ||
swap(a[0], a[size - 1 - i]; | |||
down(a, size - i, 0); | |||
a | |||
} | } | ||
} | } | ||
| Строка 248: | Строка 264: | ||
*Как и сортировка выбором, не является адаптивной. | *Как и сортировка выбором, не является адаптивной. | ||
[[Category:Базовые структуры данных | Демонстрация работы пирамидальной сортировки: | ||
* [http://www.sorting-algorithms.com/heap-sort Sorting Algorithm Animations — Heap Sort] | |||
* [http://www.cs.usfca.edu/~galles/visualization/HeapSort.html Data Structure Visualizations — Heap Sort] | |||
== Ссылки == | |||
Теория: | |||
* [http://neerc.ifmo.ru/wiki/index.php?title=%D0%94%D0%B2%D0%BE%D0%B8%D1%87%D0%BD%D0%B0%D1%8F_%D0%BA%D1%83%D1%87%D0%B0 neerc.ifmo.ru/wiki — Двоичная куча] | |||
* [http://neerc.ifmo.ru/wiki/index.php?title=%D0%A1%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B0_%D0%BA%D1%83%D1%87%D0%B5%D0%B9 neerc.ifmo.ru/wiki — Сортировка кучей] | |||
* [https://brestprog.by/topics/heap/ brestprog.by — Полное бинарное дерево. Куча. Очередь с приоритетом] | |||
* algorithmica.org — Куча. Сортировка кучей: [http://algorithmica.org/tg/quicksort 1] [https://ru.algorithmica.org/cs/basic-structures/heap/ 2] [https://ru.algorithmica.org/cs/sorting/heapsort/ 3] | |||
* [https://algs4.cs.princeton.edu/lectures/keynote/24PriorityQueues.pdf algs4.cs.princeton.edu/lectures — 2.4 Priority Queues] | |||
* [http://brilliant.org/wiki/heap-sort/ brilliant.org — Heap Sort] | |||
Демонстрация: | |||
* [https://visualgo.net/en/heap visualgo.net — Binary Heap] | |||
* [https://www.cs.usfca.edu/~galles/visualization/Heap.html www.cs.usfca.edu — Binary Heap] | |||
* [https://www.cs.usfca.edu/~galles/visualization/HeapSort.html www.cs.usfca.edu — Heap Sort] | |||
Код: | |||
* [https://github.com/indy256/codelibrary/blob/master/cpp/structures/binary_heap.cpp indy256/codelibrary/cpp/structures/binary_heap.cpp] | |||
* [https://github.com/kevin-wayne/algs4/blob/master/src/main/java/edu/princeton/cs/algs4/Heap.java kevin-wayne/algs4/Heap.java] | |||
* [https://github.com/kevin-wayne/algs4/blob/master/src/main/java/edu/princeton/cs/algs4/MaxPQ.java kevin-wayne/algs4/MaxPQ.java] | |||
* [https://github.com/kevin-wayne/algs4/blob/master/src/main/java/edu/princeton/cs/algs4/IndexMaxPQ.java kevin-wayne/algs4/IndexMaxPQ.java] | |||
Задачи: | |||
* [http://informatics.mccme.ru/course/view.php?id=18 informatics.mccme.ru — Курс «Структуры данных» — часть 2] | |||
* [http://informatics.mccme.ru/course/view.php?id=3 informatics.mccme.ru — Курс «Поиск и сортировка» — часть 5] | |||
* [[:Категория:Задачи: Очередь с приоритетами|Задачи: Очередь с приоритетами]] | |||
[[Category:Базовые структуры и абстрактные типы данных]] | |||
Текущая версия от 15:22, 24 мая 2023
TLDR
Общие сведения
Очередь с приоритетами (англ. priority queue) — абстрактный контейнер, похожий на обычную очередь, но имеющий ряд особенностей:
- Каждому элементу очереди с приоритетами сопоставлено некоторое значение, именуемое приоритетом этого элемента. Приоритеты допускают сравнение друг с другом;
- Функция извлечения из очереди с приоритетами возвращает тот элемент, приоритет которого является максимальным.
Учащийся, выполняющий домашнее задание по нескольким предметам, может вводить различные показатели, определяющие порядок выполнения: от более любимых предметов к менее любимым, от менее сложных к более сложным, и так далее. Пожарная бригада планирует выезды сообразно с категорией сложности возгорания. Операционная система компьютера выделяет аппаратные ресурсы в первую очередь приложениям, запущенным с приоритетом реального времени, и лишь затем — остальным приложениям. Эти примеры позволяют пояснить назначение и принципы функционирования очередей с приоритетами.
Интерфейс
Интерфейс очереди с приоритетами в целом аналогичен интерфейсу обычной очереди, но в операции добавления появляется второй аргумент, а операция удаления возвращает элемент с наибольшим приоритетом:
| void | enqueue(T1 value, T2 priority) | — вставка элемента value с приоритетом priority в очередь; | |
| T1 | dequeue() | — извлечение элемента с максимальным приоритетом из очереди; | |
| bool | isEmpty() | — проверка очереди на отсутствие элементов. |
Демонстрация работы
- В демонстрации показана очередь, в которой наивысший приоритет имеет наименьший элемент. Эта очередь построена на невозрастающей пирамиде (англ. min-oriented heap).
- В статье рассматривается реализация очереди, в которой наивысший приоритет имеет наибольший элемент; соответствующая ей пирамида называется неубывающей (англ. max-oriented).
Реализация
Очередь с приоритетами, построенная на обычном массиве или списке, позволяет выполнять вставку за O(1), но поиск и удаление элемента с максимальным приоритетом будут иметь сложность O(N). Существует более быстрая реализация очереди с приоритетами, подразумевающая применение особого способа организации данных, получившего название пирамиды (англ. heap, также используется термин «куча»; не следует путать с динамическим хранилищем данных в памяти, которое также именуется кучей).
Определение пирамиды
Пирамида — это двоичное дерево, для элементов которого выполняется дополнительное условие (называемое основным свойством пирамиды): значение элемента в родительском узле больше (более точно, не меньше) значений во всех узлах-потомках.
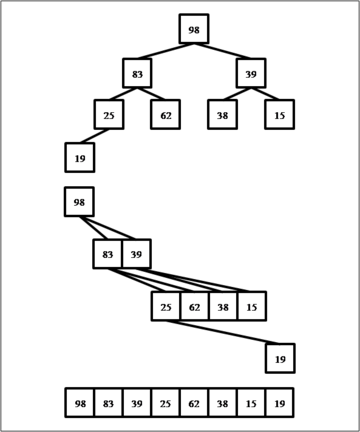
Пирамиду можно построить на массиве, используя соотношения между индексами ячеек массива для определения связей элементов. На иллюстрации показан пример пирамиды, содержащей 8 элементов, и её отображение на массив.
Если индексация элементов массива начинается с единицы, то непосредственные потомки элемента с индексом i будут иметь индексы (2 * i) и (2 * i + 1), а родителем будет являться элемент с индексом (i / 2). Так, потомками элемента с индексом 1 будут элементы с индексами 2 и 3, потомками элемента с индексом 2 — элементы с индексами 4 и 5, родителем элемента с индексом 8 будет элемент с индексом 4.
Если индексация элементов массива начинается с нуля, то непосредственные потомки элемента с индексом i будут иметь индексы (2 * i + 1) и (2 * i + 2), а родителем будет являться элемент с индексом ((i - 1) / 2). Так, потомками элемента с индексом 0 будут элементы с индексами 1 и 2, потомками элемента с индексом 1 — элементы с индексами 3 и 4, родителем элемента с индексом 7 будет элемент с индексом 3.
В целях упрощения дальнейшего кода определим вспомогательные функции parent(), leftChild() и rightChild():
int parent(int i) {
return (i - 1) / 2;
}
int leftChild(int i) {
return 2 * i + 1;
}
int rightChild(int i) {
return 2 * i + 2;
}
Пирамида в данной реализации является почти полным двоичным деревом: только самый нижний уровень может быть не заполнен полностью, и его заполнение происходит строго слева направо. Можно показать, что в N-элементной пирамиде ⌈N/2⌉ последних элементов являются листьями, то есть не имеют потомков. При индексации массива с единицы листья имеют индексы от (N / 2 + 1) до N, при индексации с нуля — от (N / 2) до (N - 1).
Высотой пирамиды называется количество рёбер на самом длинном пути от вершины пирамиды до какого-либо листа. Достаточно легко убедиться, что высота почти полной пирамиды из N элементов равна ⌊log2N⌋.
Поддержка основного свойства пирамиды
Добавление, изменение или удаление некоторого элемента пирамиды может нарушить основное свойство пирамиды. Каждое такое нарушение можно отнести к одному из двух основных типов:
- Значение элемента больше, чем у его родителя, и поэтому элемент должен занять место выше, чем имеет сейчас;
- Значение элемента меньше, чем у хотя бы одного из его потомков, и поэтому элемент должен занять место ниже, чем имеет сейчас.
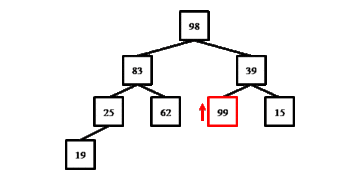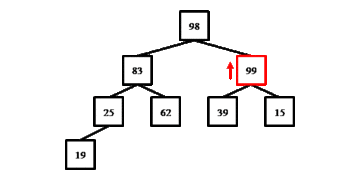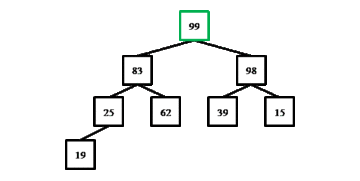
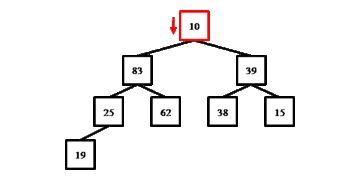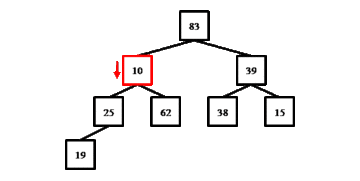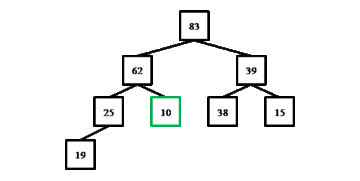
Процедура up(), которая будет исправлять нарушения первого типа, обменивает заданный элемент с его родителем до тех пор, пока значение элемента не станет меньше значения родителя, либо элемент не окажется на вершине пирамиды. Процедура принимает индекс элемента, который вызывает нарушение основного свойства пирамиды. Приведённый ниже код работает для массива, в котором индексация начинается с нуля.
void up(int i) {
while (i != 0 && a[i] > a[parent(i)]) {
swap(a[i], a[parent(i)];
i = parent(i);
}
}
Процедура down(), исправляющая нарушения второго типа, обменивает заданный элемент с максимальным из его потомков до тех пор, пока значение элемента не станет больше значений потомков, либо элемент не окажется листом. Обмен происходит с максимальным из потомков, так как только в этом случае основное свойство пирамиды гарантированно поддерживается после обмена. Как и в предыдущем случае, процедура принимает индекс неверно расположенного элемента в массиве, а индексация элементов начинается с нуля. Общее количество элементов в очереди равно size.
void down(int i) {
while (i < size / 2) {
int maxI = leftChild(i);
if (rightChild(i) < size && a[rightChild(i)] > a[leftChild(i)])
maxI = rightChild(i);
if (a[i] >= a[maxI])
return;
swap(a[i], a[maxI]);
i = maxI;
}
}
Построение очереди с приоритетами на пирамиде
Важная особенность пирамиды состоит в том, что максимальное из хранящихся в ней значений находится на её вершине. В совокупности с тем фактом, что показанные ранее операции восстановления пирамиды up() и down() производят количество перемещений, не превышающее высоты пирамиды, это позволяет разработать эффективную реализацию очередей с приоритетами.
Прежде всего, эта реализация потребует описания структуры элемента (так как элемент хранит не только приоритет, но и значение) и объявления массива, который будет организован как пирамида. Операции восстановления пирамиды должны будут сравнивать поля .priority. Для хранения количества элементов в очереди отводится отдельная переменная size, которая в конструкторе инициализируется значением 0.
static const int MAX_SIZE = 100;
struct Elem {
int val;
int priority;
Elem(int v = 0, int p = 0) {
val = v;
priority = p;
}
} a[MAX_SIZE];
int size;
Добавление элемента происходит в ячейку a[size]. Так как после добавления может быть нарушено основное свойство пирамиды, требуется дополнительно вызвать процедуру up(). Общая сложность операции добавления составит O(logN).
void enqueue(int value, int priority) {
if (size + 1 == MAX_SIZE)
/* обработка ошибки - переполнение очереди */
a[size++] = Elem(value, priority);
up(size - 1);
}
При удалении элемента можно поступить следующим образом: переместить на вершину пирамиды её последний элемент и выполнить для него операцию down(). Сложность удаления равна O(logN).
int dequeue() {
if (size == 0)
/* обработка ошибки - нет элементов для извлечения */
swap(a[0], a[--size]);
down(0);
return a[size].val;
}
Ниже приведён полный код реализации очереди с приоритетами. Переполнение и попытка извлечения из пустой очереди выявляются с помощью конструкции assert (заголовочный файл <assert.h> либо <cassert>).
class PriorityQueue {
static const int MAX_SIZE = 100;
struct Elem {
int val;
int priority;
Elem(int v = 0, int p = 0) {
val = v;
priority = p;
}
} a[MAX_SIZE];
int size;
void up(int i) {
while (i != 0 && a[i].priority > a[(i - 1) / 2].priority) {
swap(a[i], a[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
void down(int i) {
while (i < size / 2) {
int maxI = 2 * i + 1;
if (2 * i + 2 < size && a[2 * i + 2].priority > a[2 * i + 1].priority)
maxI = 2 * i + 2;
if (a[i].priority >= a[maxI].priority)
return;
swap(a[i], a[maxI]);
i = maxI;
}
}
public:
PriorityQueue() {
size = 0;
}
void enqueue(int value, int priority) {
assert(size + 1 < MAX_SIZE);
a[size++] = Elem(value, priority);
up(size - 1);
}
int dequeue() {
assert(size > 0);
swap(a[0], a[--size]);
down(0);
return a[size].val;
}
bool isEmpty() {
return size == 0;
}
};
Очередь с приоритетами в STL
В стандартной библиотеке шаблонов C++ присутствует шаблон priority_queue<T>. Для возможности его использования требуется подключить заголовочный файл <queue> и пространство имён std.
#include <iostream>
#include <queue>
using namespace std;
int main() {
priority_queue<int> pq;
q.push(1);
q.push(3);
q.push(2);
while (!s.empty()) {
cout << q.top() << ' ';
q.pop();
}
return 0; //результат "3 2 1 "
}
Упорядочение элементов в очереди производится по убыванию; в качестве операции сравнения по умолчанию используется оператор <. Для применения другой функции сравнения требуется передать её третьим параметром в конструкторе очереди (второй параметр — тип базового контейнера, по умолчанию vector). Например, определение std::priority_queue< int, std::vector<int>, std::greater<int> > позволяет получить очередь, в которой наивысшим считается минимальный приоритет (функциональный объект greater объявлен в заголовочном файле <functional>).
Набор методов для очереди с приоритетами в STL почти полностью аналогичен таковому для обычной очереди:
| priority_queue<T>() | — конструктор; | ||
| void | push(const T& x) | — добавление элемента в очередь. Приоритет элемента определяется его значением; | |
| void | pop() | — удаление элемента с максимальным приоритетом. Обратите внимание на то, что значение удаляемого элемента не возвращается; | |
| T& | top() | — получение значения элемента с максимальным приоритетом. Этот метод не производит удаление элемента; | |
| bool | empty() | — проверка очереди с приоритетами на пустоту; | |
| size_t | size() | — получение количества элементов в очереди с приоритетами. Метод возвращает беззнаковое целое число. |
Очередь с приоритетами в STL создаётся на базе шаблона последовательного контейнера с произвольным доступом (vector или deque), и для поддержания внутренней структуры она использует процедуры работы с пирамидами, определённые в заголовочном файле <algorithm>. Каждая из них принимает пару итераторов произвольного доступа It, указывающих диапазон элементов (как правило, это begin() и end(), покрывающие все элементы в контейнере). По умолчанию для сравнения во всех процедурах используется оператор <; собственный функциональный объект можно передать третьим параметром.
| void | make_heap(It first, It last) | — создание пирамиды из диапазона элементов [first, last); | |
| void | push_heap(It first, It last) | — добавление элемента, находящегося перед last, в пирамиду [first, last-1), так что весь диапазон [first, last) становится пирамидой; | |
| void | pop_heap(It first, It last) | — перемещение элемента с максимальным приоритетом (на который изначально указывает first) в конец и формирование пирамиды в диапазоне [first, last-1) из оставшихся элементов; | |
| void | sort_heap(It first, It last) | — преобразование пирамиды [first, last) в упорядоченный интервал. После вызова процедуры диапазон перестаёт быть пирамидой. |
Пирамидальная сортировка
Пирамидальная сортировка (англ. heapsort) — улучшенная версия сортировки выбором. Обычная сортировка выбором предполагает, что N раз из данного массива извлекается наименьший элемент и ставится на соответствующее место. Если для выбора наименьшего элемента используется последовательный поиск, то каждый раз просматривается весь массив, что даёт сложность каждой итерации O(N) и итоговую сложность O(N2)
Вместо последовательного поиска наименьшего элемента можно использовать пирамиду, позволяющую на каждом шаге извлекать минимальный элемент за O(1) и восстанавливаться за O(logN), что даст итоговую сложность O(NlogN). Чтобы не перемещать саму пирамиду, на каждом шаге можно извлекать максимальный элемент и перемещать его в конец. Построить пирамиду на непустом данном массиве можно двумя способами:
- Проходя от начала массива до конца, последовательно выполнить для каждого элемента операцию up() (что в целом аналогично построению очереди с приоритетами за счёт выполнения операции enqueue() для каждого элемента массива). Сложность O(NlogN);
- Построить пирамиду «снизу вверх», проходя от конца массива до начала и вызывая процедуру down() для всех элементов. Вызов down() для листьев не предусматривает никаких действий, поэтому можно начинать цикл с (size / 2 - 1). В нескольких источниках, в том числе в книге Т. Кормена «Алгоритмы: построение и анализ», показано, что сложность данного метода снижается до O(N).
Пусть функция down() использует значения a[] и size, переданные ей через параметры. Тогда код пирамидальной сортировки имеет следующий вид:
void heapsort(int a[], int size) {
for (int i = size / 2 - 1; i >= 0; i--)
down(a, size, i);
for (int i = 0; i < size; i++) {
swap(a[0], a[size - 1 - i];
down(a, size - i, 0);
}
}
Свойства пирамидальной сортировки:
- Сложность O(NlogN);
- Как и сортировка выбором, не требует дополнительной памяти, в отличие от, например, сортировки слиянием;
- Как и сортировка выбором, не является стабильной (например, массив [1-a, 1-b], где числа являются ключами, после сортировки примет вид [1-b, 1-a]);
- Как и сортировка выбором, не является адаптивной.
Демонстрация работы пирамидальной сортировки:
Ссылки
Теория:
- neerc.ifmo.ru/wiki — Двоичная куча
- neerc.ifmo.ru/wiki — Сортировка кучей
- brestprog.by — Полное бинарное дерево. Куча. Очередь с приоритетом
- algorithmica.org — Куча. Сортировка кучей: 1 2 3
- algs4.cs.princeton.edu/lectures — 2.4 Priority Queues
- brilliant.org — Heap Sort
Демонстрация:
Код:
- indy256/codelibrary/cpp/structures/binary_heap.cpp
- kevin-wayne/algs4/Heap.java
- kevin-wayne/algs4/MaxPQ.java
- kevin-wayne/algs4/IndexMaxPQ.java
Задачи: