Дерево отрезков: различия между версиями
Ctrlalt (обсуждение | вклад) |
Ctrlalt (обсуждение | вклад) Нет описания правки |
||
| (не показано 12 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
== Запрос на отрезке и модификация отдельных элементов == | == Запрос на отрезке и модификация отдельных элементов == | ||
| Строка 25: | Строка 26: | ||
|} | |} | ||
int t[ | struct SegmentTree { | ||
int size; | |||
vector<long long> t; | |||
void build(int v, int vl, int vr, vector<int> &a) { | |||
if (vl == vr) { | |||
t[v] = a[vl]; | |||
return; | |||
} | |||
int vm = vl + (vr - vl) / 2; | |||
build(2 * v + 1, vl, vm, a); | |||
build(2 * v + 2, vm + 1, vr, a); | |||
t[v] = t[2 * v + 1] + t[2 * v + 2]; | |||
} | |||
long long query(int v, int vl, int vr, int l, int r) { | |||
if (vr < l || r < vl) | |||
return 0; | |||
if (l <= vl && vr <= r) | |||
return t[v]; | |||
int vm = vl + (vr - vl) / 2; | |||
long long ql = query(2 * v + 1, vl, vm, l, r); | |||
long long qr = query(2 * v + 2, vm + 1, vr, l, r); | |||
return ql + qr; | |||
} | |||
void modify(int v, int vl, int vr, int index, int value) { | |||
if (vr < index || index < vl) | |||
t[v] = | return; | ||
if (vl == vr) { | |||
t[v] += value; | |||
return; | |||
} | |||
int vm = vl + (vr - vl) / 2; | |||
modify(2 * v + 1, vl, vm, index, value); | |||
modify(2 * v + 2, vm + 1, vr, index, value); | |||
t[v] = t[2 * v + 1] + t[2 * v + 2]; | |||
} | |||
SegmentTree(vector<int> &a) : | |||
size(a.size()), t(4 * a.size()) { | |||
build(0, 0, size - 1, a); | |||
} | } | ||
long long getSum(int l, int r) { | |||
return query(0, 0, size - 1, l, r); | |||
return | } | ||
void addValue(int index, int value) { | |||
modify(0, 0, size - 1, index, value); | |||
} | } | ||
}; | |||
} | |||
== Запрос на отрезке и модификация на отрезке == | == Запрос на отрезке и модификация на отрезке == | ||
| Строка 67: | Строка 84: | ||
* Перед выводом результата или передачей запроса будем спускать значение <tt>add[v]</tt> потомкам текущей вершины при помощи функции <tt>push()</tt>. | * Перед выводом результата или передачей запроса будем спускать значение <tt>add[v]</tt> потомкам текущей вершины при помощи функции <tt>push()</tt>. | ||
int t[ | struct SegmentTree { | ||
int size; | |||
vector<long long> t, tAdd; | |||
void build(int v, int vl, int vr, vector<int> &a) { | |||
if (vl == vr) { | |||
t[v] = a[vl]; | |||
return; | |||
} | |||
int vm = vl + (vr - vl) / 2; | |||
build(2 * v + 1, vl, vm, a); | |||
build(2 * v + 2, vm + 1, vr, a); | |||
t[v] = t[2 * v + 1] + t[2 * v + 2]; | |||
} | |||
void push(int v, int vl, int vr) { | |||
if (tAdd[v]) { | |||
t[v] += (vr - vl + 1) * tAdd[v]; | |||
if (vl < vr) { | |||
tAdd[2 * v + 1] += tAdd[v]; | |||
tAdd[2 * v + 2] += tAdd[v]; | |||
} | |||
tAdd[v] = 0; | |||
} | |||
} | |||
long long query(int v, int vl, int vr, int l, int r) { | |||
push(v, vl, vr); | |||
if (vr < l || r < vl) | |||
return 0; | |||
if (l <= vl && vr <= r) | |||
return t[v]; | |||
int vm = vl + (vr - vl) / 2; | |||
long long ql = query(2 * v + 1, vl, vm, l, r); | |||
long long qr = query(2 * v + 2, vm + 1, vr, l, r); | |||
return ql + qr; | |||
} | |||
void modify(int v, int vl, int vr, int l, int r, int value) { | |||
push(v, vl, vr); | |||
if (vr < l || r < vl) | |||
return; | |||
if (l <= vl && vr <= r) { | |||
tAdd[v] += value; | |||
push(v, vl, vr); | |||
return; | |||
} | |||
int vm = vl + (vr - vl) / 2; | |||
modify(2 * v + 1, vl, vm, l, r, value); | |||
modify(2 * v + 2, vm + 1, vr, l, r, value); | |||
t[v] = t[2 * v + 1] + t[2 * v + 2]; | |||
} | |||
SegmentTree(vector<int> &a) : | |||
size(a.size()), t(4 * a.size()), tAdd(4 * a.size()) { | |||
build(0, 0, size - 1, a); | |||
} | |||
long long getSum(int l, int r) { | |||
return query(0, 0, size - 1, l, r); | |||
} | } | ||
void addValue(int l, int r, int value) { | |||
modify(0, 0, size - 1, l, r, value); | |||
} | } | ||
}; | |||
== Почему для хранения дерева отрезков требуется массив размера 4n? == | |||
Пусть для массива a[] из n элементов создаётся дерево отрезков, хранящееся в массиве t[]. Правило требует, чтобы размер массива t[] был не менее 4n. | |||
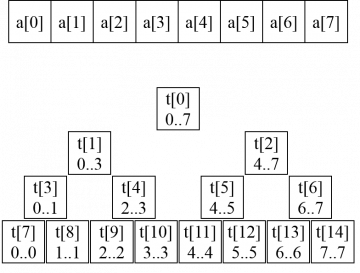
[[Файл:Segment_tree_8.png|thumb|right|360px|Дерево отрезков для массива из 8 элементов требует 15 элементов]] | |||
Однако можно рассуждать следующим образом: двоичным деревом с наибольшим количеством элементов является полное двоичное дерево. Если количество листьев в полном двоичном дереве равно n, то общее количество вершин в нём равно 2n - 1. Возможно ли, что для хранения дерева отрезков всегда будет достаточно массива размера 2n? | |||
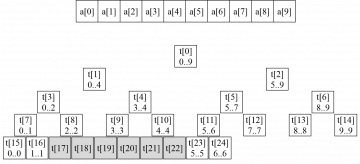
[[Файл:Segment_tree_10.png|thumb|right|360px|Дерево отрезков для массива из 10 элементов требует 25 элементов]] | |||
К сожалению, это не так. Процедура build не обязательно формирует полное двоичное дерево; некоторые элементы массива t[] могут не использоваться. Например, если n = 5, то дерево отрезков имеет высоту 4 и содержит 9 элементов. Если N = 10, объединяются два таких дерева высоты 4, и на нижнем уровне появляются 6 неиспользуемых элементов (t[17]..t[22]). | |||
Оценим более точно требуемый размер массива t[]. | |||
Прежде всего определим вспомогательные функции leftHalf(n) и rightHalf(n), возвращающие размер левого и правого поддеревьев дерева отрезков для массива a[] из n элементов (n > 1). Если n чётно, то обе функции возвращают n / 2. Если n нечётно, то средний элемент относится к левой части. | |||
int leftHalf(int n) { | |||
return n / 2 + n % 2; | |||
} | } | ||
int | int rightHalf(int n) { | ||
return n / 2; | |||
} | |||
Далее определим функцию height(n), возвращающую высоту дерева отрезков для массива a[] из n элементов. Если n = 1, то height(n) = 1. В других случаях height(n) = 1 + max(height(leftHalf(n)), height(rightHalf(n))); так как левое поддерево всегда не меньше правого, эту запись можно упростить: height(n) = 1 + height(leftHalf(n)). | |||
Кроме того, определим функцию fullSize(h), возвращающую размер полного двоичного дерева высоты h. | |||
int height(int n) { | |||
return | if (n == 1) | ||
return 1; | |||
else | |||
return 1 + height(leftHalf(n)); | |||
} | } | ||
int fullSize(int h) { | |||
return (1 << h) - 1; | |||
} | |||
if ( | Наконец, определим функцию tSize(n), возвращающую размер t[] для массива a[] из n элементов. Если n = 1, то tSize(n) = 1. Далее, если левое и правое поддерево имеют одинаковую высоту, то необходимый размер t[] определяется последним (нижним) элементом правого поддерева, а левое поддерево становится полным: tSize(n) = 1 + fullSize(height(leftHalf(n))) + tSize(rightHalf(n)). Если же левое поддерево выше правого, то необходимый размер t[] определяется последним (нижним) элементом левого поддерева, а правое поддерево становится полным: tSize(n) = 1 + tSize(leftHalf(n)) + fullSize(height(rightHalf(n))). | ||
int tSize(int n) { | |||
return; | if (n == 1) | ||
return 1; | |||
int | int leftHeight = height(leftHalf(n)), rightHeight = height(rightHalf(n)); | ||
if (leftHeight == rightHeight) | |||
return 1 + fullSize(leftHeight) + tSize(rightHalf(n)); | |||
else | |||
return 1 + tSize(leftHalf(n)) + fullSize(rightHeight); | |||
} | } | ||
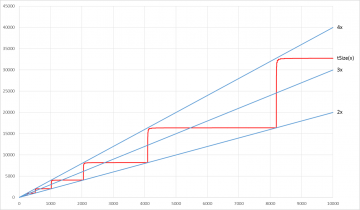
[[Файл:tSize.png|thumb|right|360px|Функции tSize(x), 2x, 3x, 4x]] | |||
Можно видеть, что график функции tSize практически всегда находится выше графика функции 2x и всегда ниже графика функции 4x. Например, tSize(8448) = 32705, что значительно превышает не только удвоенный, но и утроенный размер исходного массива. | |||
* [http:// | * [http://www.quora.com/Why-does-4-*-N-space-have-to-be-allocated-for-a-segment-tree-where-N-is-the-size-of-the-original-array Quora.com — Why does 4 * N space have to be allocated for a segment tree, where N is the size of the original array?] | ||
* | |||
* | |||
== Ссылки == | == Ссылки == | ||
Теория: | |||
* Codeforces EDU — Дерево отрезков: [https://codeforces.com/edu/course/2/lesson/4 часть 1], [https://codeforces.com/edu/course/2/lesson/5 часть 2] | |||
* [http://e-maxx.ru/algo/segment_tree e-maxx.ru — Дерево отрезков] | * [http://e-maxx.ru/algo/segment_tree e-maxx.ru — Дерево отрезков] | ||
* [http://neerc.ifmo.ru/wiki/index.php?title=%D0%94%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0,_%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC%D1%8B_%D0%B8_%D1%81%D1%82%D1%80%D1%83%D0%BA%D1%82%D1%83%D1%80%D1%8B_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85#.D0.94.D0.B5.D1.80.D0.B5.D0.B2.D0.BE_.D0.BE.D1.82.D1.80.D0.B5.D0.B7.D0.BA.D0.BE.D0.B2 neerc.ifmo.ru/wiki — Дерево отрезков] | * [http://neerc.ifmo.ru/wiki/index.php?title=%D0%94%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0,_%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC%D1%8B_%D0%B8_%D1%81%D1%82%D1%80%D1%83%D0%BA%D1%82%D1%83%D1%80%D1%8B_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85#.D0.94.D0.B5.D1.80.D0.B5.D0.B2.D0.BE_.D0.BE.D1.82.D1.80.D0.B5.D0.B7.D0.BA.D0.BE.D0.B2 neerc.ifmo.ru/wiki — Дерево отрезков] | ||
* [http:// | * [https://brestprog.by/topics/segmenttree/ brestprog — Дерево отрезков] | ||
* [http://visualgo.net/segmenttree | * [http://opentrains.mipt.ru/zksh/files/zksh2015/lectures/mipt-2014-burunduk1-ds.pdf Копелиович С. Лекция про структуры данных Зимней школы МФТИ] | ||
* [http://github.com/indy256/codelibrary/blob/ | * [http://i.cs.hku.hk/~provinci/training2015/notes3.pdf i.cs.hku.hk — Segment Trees: Applications] | ||
* [http://sharmaeklavya2.github.io/blog/generalizing-segment-trees.html sharmaeklavya2.github.io — Generalizing Segment Trees] | |||
* [https://arxiv.org/pdf/1811.01226.pdf Ibtehaz N. Multidimensional segment trees can do range queries and updates in logarithmic time] | |||
Демонстрация: | |||
* [https://visualgo.net/en/segmenttree VisuAlgo — Segment Tree] | |||
Код: | |||
* [http://github.com/indy256/codelibrary/blob/9f99e9476b1435fb6ccaea6e1b83684bc5af3ef1/java/src/SegmentTree.java CodeLibrary — Segment Tree with interval modification] | |||
* [http://github.com/indy256/codelibrary/blob/9f99e9476b1435fb6ccaea6e1b83684bc5af3ef1/java/src/SegmentTreeFast.java CodeLibrary — Segment Tree with interval modification without recursion] | |||
* [http://github.com/ADJA/algos/blob/master/DataStructures/SegmentTree(Assign-Sum).cpp Algos — Segment Tree (Assign-Sum)] | * [http://github.com/ADJA/algos/blob/master/DataStructures/SegmentTree(Assign-Sum).cpp Algos — Segment Tree (Assign-Sum)] | ||
* [http://github.com/ADJA/algos/blob/master/DataStructures/ImplicitSegmentTree.cpp Algos — Implicit segment tree] | |||
Задачи: | |||
* [http://informatics.mccme.ru/py-source/source/dir/420 informatics.mccme.ru — Тема «Дерево отрезков, RSQ, RMQ»] | |||
* Задачи Зимней школы МФТИ: [http://opentrains.mipt.ru/zksh/files/zksh2015/lectures/zksh_segtree_tasks_C.pdf группа C], [http://opentrains.mipt.ru/zksh/files/zksh2015/lectures/zksh_segtree_tasks_B.pdf группа B], [http://opentrains.mipt.ru/zksh/files/zksh2015/lectures/zksh_segtree_tasks_A.pdf группа A] | |||
* [[:Категория:Задачи: Дерево отрезков|Задачи: Дерево отрезков]] | |||
[[Category:Структуры данных для задач RSQ/RMQ]] | [[Category:Структуры данных для задач RSQ/RMQ]] | ||
Текущая версия от 17:58, 18 февраля 2023
Запрос на отрезке и модификация отдельных элементов
- Если отрезок текущей вершины не пересекается с отрезком запроса, то возвращается нейтральное значение.
- Если отрезок текущей вершины целиком включён в отрезок запроса, то возвращается значение, хранящееся в текущей вершине.
- Во всех остальных случаях запрос перенаправляется потомкам текущей вершины.
Можно выделить два распространённых способа реализации данной логики:
if (r < vl || vr < l)
//отрезки не пересекаются
if (l <= vl && vr <= r)
//отрезок текущей вершины принадлежит отрезку запроса
query(2 * v + 1, vl, vm, l, r);
query(2 * v + 2, vm + 1, vr, l, r);
|
if (l > r)
//отрезки не пересекаются
if (l == vl && vr == r)
//отрезок текущей вершины принадлежит отрезку запроса
query(2 * v + 1, vl, vm, l, min(r, vm));
query(2 * v + 2, vm + 1, vr, max(l, vm + 1), r);
|
struct SegmentTree {
int size;
vector<long long> t;
void build(int v, int vl, int vr, vector<int> &a) {
if (vl == vr) {
t[v] = a[vl];
return;
}
int vm = vl + (vr - vl) / 2;
build(2 * v + 1, vl, vm, a);
build(2 * v + 2, vm + 1, vr, a);
t[v] = t[2 * v + 1] + t[2 * v + 2];
}
long long query(int v, int vl, int vr, int l, int r) {
if (vr < l || r < vl)
return 0;
if (l <= vl && vr <= r)
return t[v];
int vm = vl + (vr - vl) / 2;
long long ql = query(2 * v + 1, vl, vm, l, r);
long long qr = query(2 * v + 2, vm + 1, vr, l, r);
return ql + qr;
}
void modify(int v, int vl, int vr, int index, int value) {
if (vr < index || index < vl)
return;
if (vl == vr) {
t[v] += value;
return;
}
int vm = vl + (vr - vl) / 2;
modify(2 * v + 1, vl, vm, index, value);
modify(2 * v + 2, vm + 1, vr, index, value);
t[v] = t[2 * v + 1] + t[2 * v + 2];
}
SegmentTree(vector<int> &a) :
size(a.size()), t(4 * a.size()) {
build(0, 0, size - 1, a);
}
long long getSum(int l, int r) {
return query(0, 0, size - 1, l, r);
}
void addValue(int index, int value) {
modify(0, 0, size - 1, index, value);
}
};
Запрос на отрезке и модификация на отрезке
- Считаем, что актуальное значение в вершине v равно t[v] + add[v] * (vr - vl + 1).
- Перед выводом результата или передачей запроса будем спускать значение add[v] потомкам текущей вершины при помощи функции push().
struct SegmentTree {
int size;
vector<long long> t, tAdd;
void build(int v, int vl, int vr, vector<int> &a) {
if (vl == vr) {
t[v] = a[vl];
return;
}
int vm = vl + (vr - vl) / 2;
build(2 * v + 1, vl, vm, a);
build(2 * v + 2, vm + 1, vr, a);
t[v] = t[2 * v + 1] + t[2 * v + 2];
}
void push(int v, int vl, int vr) {
if (tAdd[v]) {
t[v] += (vr - vl + 1) * tAdd[v];
if (vl < vr) {
tAdd[2 * v + 1] += tAdd[v];
tAdd[2 * v + 2] += tAdd[v];
}
tAdd[v] = 0;
}
}
long long query(int v, int vl, int vr, int l, int r) {
push(v, vl, vr);
if (vr < l || r < vl)
return 0;
if (l <= vl && vr <= r)
return t[v];
int vm = vl + (vr - vl) / 2;
long long ql = query(2 * v + 1, vl, vm, l, r);
long long qr = query(2 * v + 2, vm + 1, vr, l, r);
return ql + qr;
}
void modify(int v, int vl, int vr, int l, int r, int value) {
push(v, vl, vr);
if (vr < l || r < vl)
return;
if (l <= vl && vr <= r) {
tAdd[v] += value;
push(v, vl, vr);
return;
}
int vm = vl + (vr - vl) / 2;
modify(2 * v + 1, vl, vm, l, r, value);
modify(2 * v + 2, vm + 1, vr, l, r, value);
t[v] = t[2 * v + 1] + t[2 * v + 2];
}
SegmentTree(vector<int> &a) :
size(a.size()), t(4 * a.size()), tAdd(4 * a.size()) {
build(0, 0, size - 1, a);
}
long long getSum(int l, int r) {
return query(0, 0, size - 1, l, r);
}
void addValue(int l, int r, int value) {
modify(0, 0, size - 1, l, r, value);
}
};
Почему для хранения дерева отрезков требуется массив размера 4n?
Пусть для массива a[] из n элементов создаётся дерево отрезков, хранящееся в массиве t[]. Правило требует, чтобы размер массива t[] был не менее 4n.
Однако можно рассуждать следующим образом: двоичным деревом с наибольшим количеством элементов является полное двоичное дерево. Если количество листьев в полном двоичном дереве равно n, то общее количество вершин в нём равно 2n - 1. Возможно ли, что для хранения дерева отрезков всегда будет достаточно массива размера 2n?
К сожалению, это не так. Процедура build не обязательно формирует полное двоичное дерево; некоторые элементы массива t[] могут не использоваться. Например, если n = 5, то дерево отрезков имеет высоту 4 и содержит 9 элементов. Если N = 10, объединяются два таких дерева высоты 4, и на нижнем уровне появляются 6 неиспользуемых элементов (t[17]..t[22]).
Оценим более точно требуемый размер массива t[].
Прежде всего определим вспомогательные функции leftHalf(n) и rightHalf(n), возвращающие размер левого и правого поддеревьев дерева отрезков для массива a[] из n элементов (n > 1). Если n чётно, то обе функции возвращают n / 2. Если n нечётно, то средний элемент относится к левой части.
int leftHalf(int n) {
return n / 2 + n % 2;
}
int rightHalf(int n) {
return n / 2;
}
Далее определим функцию height(n), возвращающую высоту дерева отрезков для массива a[] из n элементов. Если n = 1, то height(n) = 1. В других случаях height(n) = 1 + max(height(leftHalf(n)), height(rightHalf(n))); так как левое поддерево всегда не меньше правого, эту запись можно упростить: height(n) = 1 + height(leftHalf(n)).
Кроме того, определим функцию fullSize(h), возвращающую размер полного двоичного дерева высоты h.
int height(int n) {
if (n == 1)
return 1;
else
return 1 + height(leftHalf(n));
}
int fullSize(int h) {
return (1 << h) - 1;
}
Наконец, определим функцию tSize(n), возвращающую размер t[] для массива a[] из n элементов. Если n = 1, то tSize(n) = 1. Далее, если левое и правое поддерево имеют одинаковую высоту, то необходимый размер t[] определяется последним (нижним) элементом правого поддерева, а левое поддерево становится полным: tSize(n) = 1 + fullSize(height(leftHalf(n))) + tSize(rightHalf(n)). Если же левое поддерево выше правого, то необходимый размер t[] определяется последним (нижним) элементом левого поддерева, а правое поддерево становится полным: tSize(n) = 1 + tSize(leftHalf(n)) + fullSize(height(rightHalf(n))).
int tSize(int n) {
if (n == 1)
return 1;
int leftHeight = height(leftHalf(n)), rightHeight = height(rightHalf(n));
if (leftHeight == rightHeight)
return 1 + fullSize(leftHeight) + tSize(rightHalf(n));
else
return 1 + tSize(leftHalf(n)) + fullSize(rightHeight);
}
Можно видеть, что график функции tSize практически всегда находится выше графика функции 2x и всегда ниже графика функции 4x. Например, tSize(8448) = 32705, что значительно превышает не только удвоенный, но и утроенный размер исходного массива.
Ссылки
Теория:
- Codeforces EDU — Дерево отрезков: часть 1, часть 2
- e-maxx.ru — Дерево отрезков
- neerc.ifmo.ru/wiki — Дерево отрезков
- brestprog — Дерево отрезков
- Копелиович С. Лекция про структуры данных Зимней школы МФТИ
- i.cs.hku.hk — Segment Trees: Applications
- sharmaeklavya2.github.io — Generalizing Segment Trees
- Ibtehaz N. Multidimensional segment trees can do range queries and updates in logarithmic time
Демонстрация:
Код:
- CodeLibrary — Segment Tree with interval modification
- CodeLibrary — Segment Tree with interval modification without recursion
- Algos — Segment Tree (Assign-Sum)
- Algos — Implicit segment tree
Задачи:
- informatics.mccme.ru — Тема «Дерево отрезков, RSQ, RMQ»
- Задачи Зимней школы МФТИ: группа C, группа B, группа A
- Задачи: Дерево отрезков