Множество. Реализация на битовых векторах: различия между версиями
Ctrlalt (обсуждение | вклад) |
Ctrlalt (обсуждение | вклад) |
||
| (не показано 25 промежуточных версий этого же участника) | |||
| Строка 5: | Строка 5: | ||
Минимальный набор функций, обеспечиваемый множеством, содержит следующие операции: | Минимальный набор функций, обеспечиваемый множеством, содержит следующие операции: | ||
{| | {| class="methodlist" | ||
| | | || void || insert(T value) || — добавление значения <tt>value</tt> в множество; | ||
|- | |- | ||
| | | || void || remove(T value) || — исключение значения <tt>value</tt> из множества; | ||
|- | |- | ||
| | | || bool || contains(T value) || — проверка на вхождение значения <tt>value</tt> в множество. | ||
|} | |} | ||
| Строка 16: | Строка 16: | ||
== Демонстрация работы == | == Демонстрация работы == | ||
[ | * [http://visualgo.net/bitmask.html VisuAlgo — Bitmask] | ||
== Реализация | == Реализация на логическом массиве == | ||
В тех случаях, когда диапазон значений для множества сравнительно мал, становится возможным определить для каждого допустимого значения отдельную переменную, которая будет указывать на то, содержится ли соответствующее ей значение в множестве. Пусть, например, необходимо реализовать множество строчных латинских символов и десятичных цифр. Так как общее число различных элементов равно 36, для каждого из них можно выделить отдельную логическую переменную. Значение «истина» такой переменной будет свидетельствовать о присутствии соответствующего символа в множестве, значение «ложь» — об его отсутствии. | В тех случаях, когда диапазон значений для множества сравнительно мал, становится возможным определить для каждого допустимого значения отдельную переменную, которая будет указывать на то, содержится ли соответствующее ей значение в множестве. Пусть, например, необходимо реализовать множество строчных латинских символов и десятичных цифр. Так как общее число различных элементов равно 36, для каждого из них можно выделить отдельную логическую переменную. Значение «истина» такой переменной будет свидетельствовать о присутствии соответствующего символа в множестве, значение «ложь» — об его отсутствии. | ||
| Строка 35: | Строка 33: | ||
Set() { | Set() { | ||
for (int i = 0; i < 36; i++) | for (int i = 0; i < 36; i++) | ||
a[i | a[i] = false; | ||
} | } | ||
| Строка 57: | Строка 55: | ||
Однако данная реализация имеет существенный недостаток: так как <tt>sizeof(bool) ≥ sizeof(char)</tt>, массив логических переменных занимает не менее 36 байт = 288 бит, тогда как каждая переменная несёт 1 бит информации, так что весь массив требует 36 бит. | Однако данная реализация имеет существенный недостаток: так как <tt>sizeof(bool) ≥ sizeof(char)</tt>, массив логических переменных занимает не менее 36 байт = 288 бит, тогда как каждая переменная несёт 1 бит информации, так что весь массив требует 36 бит. | ||
== | == Реализация на битовом векторе == | ||
Добиться сокращения объёма используемой памяти можно за счёт манипуляций непосредственно с битами. В этом случае для представления рассмотренного выше множества понадобится 36 бит. Существует несколько возможностей выделить в памяти последовательный блок такого размера: | Добиться сокращения объёма используемой памяти можно за счёт манипуляций непосредственно с битами. В этом случае для представления рассмотренного выше множества понадобится 36 бит. Существует несколько возможностей выделить в памяти последовательный блок такого размера: | ||
| Строка 63: | Строка 61: | ||
*Представление переменными типа <tt>short</tt> даёт массив из 3 элементов, при этом (16 * 3 - 36 = 12) бит будут неиспользуемыми; | *Представление переменными типа <tt>short</tt> даёт массив из 3 элементов, при этом (16 * 3 - 36 = 12) бит будут неиспользуемыми; | ||
*Представление переменными типа <tt>long</tt> даёт массив из 2 элементов, при этом (32 * 2 - 36 = 28) бит будут неиспользуемыми. | *Представление переменными типа <tt>long</tt> даёт массив из 2 элементов, при этом (32 * 2 - 36 = 28) бит будут неиспользуемыми. | ||
[[Файл:bitset_alloc.png|360px|thumb|360px|right|Представление 36 бит памяти переменными различных типов]] | |||
Минимальный размер памяти, адресуемый с помощью переменной в языке C++, ограничен размером типа <tt>char</tt>. Поэтому при реализации битовой последовательности, длина которой не кратна <tt>sizeof(char)</tt>, неизбежно появление избыточных битов; их количество тем меньше, чем меньше размер используемого типа данных. | Минимальный размер памяти, адресуемый с помощью переменной в языке C++, ограничен размером типа <tt>char</tt>. Поэтому при реализации битовой последовательности, длина которой не кратна <tt>sizeof(char)</tt>, неизбежно появление избыточных битов; их количество тем меньше, чем меньше размер используемого типа данных. | ||
| Строка 70: | Строка 70: | ||
Для изменения некоторого бита в битовом векторе требуется соответствующим образом модифицировать элемент массива, содержащий этот бит. Установить, какой ячейке массива принадлежит бит с номером <tt>i</tt> (нумерация с нуля слева направо), достаточно просто: она будет иметь индекс <tt>(i / sizeof(T))</tt>, где <tt>T</tt> — используемый тип элементов. Внутри ячейки искомый бит будет иметь смещение <tt>(i % sizeof(T))</tt>. Важно, чтобы все остальные биты сохранили свои прежние значения; добиться подобного результата можно с помощью битовых операций языка C++. Битовые операции отличаются от соответствующих логических операций тем, что они применяются последовательно к каждой паре битов значений-операндов, вследствие чего результатом этих операций является новое целочисленное значение. Логические и битовые операции языка C++ описаны в следующей таблице. | Для изменения некоторого бита в битовом векторе требуется соответствующим образом модифицировать элемент массива, содержащий этот бит. Установить, какой ячейке массива принадлежит бит с номером <tt>i</tt> (нумерация с нуля слева направо), достаточно просто: она будет иметь индекс <tt>(i / sizeof(T))</tt>, где <tt>T</tt> — используемый тип элементов. Внутри ячейки искомый бит будет иметь смещение <tt>(i % sizeof(T))</tt>. Важно, чтобы все остальные биты сохранили свои прежние значения; добиться подобного результата можно с помощью битовых операций языка C++. Битовые операции отличаются от соответствующих логических операций тем, что они применяются последовательно к каждой паре битов значений-операндов, вследствие чего результатом этих операций является новое целочисленное значение. Логические и битовые операции языка C++ описаны в следующей таблице. | ||
{| cellspacing="10" | {| cellspacing="10" class="centered middled" | ||
| | | || NOT (отрицание) || AND (конъюнкция) || OR (дизъюнкция) || XOR (исключающее ИЛИ) | ||
| | |- | ||
| | | Таблица истинности | ||
| | |||
| | |||
|- | |||
| | | | ||
{| | {| align="center" class="standard centered w60px" | ||
| A || not A | |||
|- | |- | ||
| 0 || 1 | |||
|- | |- | ||
| 1 || 0 | |||
|} | |} | ||
| | | | ||
{| | {| align="center" class="standard centered w60px" | ||
| A || B || A and B | |||
|- | |- | ||
| 0 || 0 || 0 | |||
|- | |- | ||
| 0 || 1 || 0 | |||
|- | |- | ||
| 1 || 0 || 0 | |||
|- | |- | ||
| 1 || 1 || 1 | |||
|} | |} | ||
| | | | ||
{| | {| align="center" class="standard centered w60px" | ||
| A || B || A or B | |||
|- | |- | ||
| 0 || 0 || 0 | |||
|- | |- | ||
| 0 || 1 || 1 | |||
|- | |- | ||
| 1 || 0 || 1 | |||
|- | |- | ||
| 1 || 1 || 1 | |||
|} | |} | ||
| | |||
{| | {| align="center" class="standard centered w60px" | ||
| A || B || A xor B | |||
|- | |- | ||
| 0 || 0 || 0 | |||
|- | |- | ||
| 0 || 1 || 1 | |||
|- | |- | ||
| 1 || 0 || 1 | |||
|- | |- | ||
| 1 || 1 || 0 | |||
|} | |} | ||
|- | |- | ||
| Логическая операция<br>в С++ | |||
| | | | ||
// ! | // ! | ||
| Строка 160: | Строка 156: | ||
r2 = a2 || b2; | r2 = a2 || b2; | ||
//r2 == 1 | //r2 == 1 | ||
| | | отсутствует;<br>для логических переменных<br>эквивалентом является<tt>!=</tt> | ||
|- | |||
| Битовая операция<br>в С++ | |||
| | |||
// ~ | |||
short a = 123, | |||
r = ~a; | |||
//r == -124 | |||
/* | |||
123: 0000000001111011 | |||
-124: 1111111110000100 | |||
*/ | |||
| | |||
// & | |||
short a = 123, | |||
b = 358, | |||
r = a & b; | |||
//r == 98 | |||
/* | |||
123: 0000000001111011 | |||
358: 0000000101100110 | |||
98: 0000000001100010 | |||
*/ | |||
| | |||
// | | |||
short a = 123, | |||
b = 358, | |||
r = a | b; | |||
//r == 383 | |||
/* | |||
123: 0000000001111011 | |||
358: 0000000101100110 | |||
383: 0000000101111111 | |||
*/ | |||
| | |||
// ^ | |||
short a = 123, | |||
b = 358, | |||
r = a ^ b; | |||
//r == 285 | |||
/* | |||
123: 0000000001111011 | |||
358: 0000000101100110 | |||
285: 0000000100011101 | |||
*/ | |||
|} | |} | ||
Из таблиц истинности битовых операций можно вывести ряд важных утверждений: | |||
*Конъюнкция бита с единичным битом не изменяет его значение; | |||
*Конъюнкция бита с нулевым битом меняет его значение на 0; | |||
*Дизъюнкция бита с единичным битом меняет его значение на 1; | |||
*Дизъюнкция бита с нулевым битом не изменяет его значение. | |||
=== Установка значения указанного бита в единицу === | |||
Здесь и далее будем предполагать, что битовый вектор построен на массиве переменных типа <tt>char</tt>, размер которого равен 1 байт. Пусть требуется установить значение 20-го бита в единицу (это, например, будет являться признаком вхождения символа <tt>'u'</tt> в рассмотренное выше множество). 20-й бит находится в ячейке с индексом (20 / 8 = 2) и имеет смещение (20 % 8 = 4). Эта ячейка в памяти имеет следующий вид: | |||
xxxxxxxx | |||
Здесь <tt>x</tt> — любое битовое значение (ноль или единица). Значение данной ячейки нужно изменить таким образом, чтобы она приобрела вид | |||
xxxx1xxx | |||
Утверждения, полученные в ходе анализа битовых операций, помогают понять, что для установки значения бита в единицу требуется выполнить побитовую дизъюнкцию содержащей его ячейки со специальным вспомогательным значением, называемым маской. Размер маски должен быть равен размеру ячейки, все биты маски кроме того, который имеет то же смещение, что и модифицируемый бит, должны быть нулевыми, а оставшийся бит — единичным: | |||
xxxxxxxx | | |||
00001000 | |||
= xxxx1xxx | |||
Сформировать необходимую для дизъюнкции маску можно, применив к константе 1 (которая имеет битовое представление 00000001) операцию битового сдвига влево (<tt><<</tt>). Количество разрядов, на которое осуществляется сдвиг, определяется следующим образом. Единичный бит должен иметь определённое смещение (для 20-го бита равное 4), отсчитываемое от левой границы ячейки. Для того чтобы единичный бит оказался у левой границы ячейки, константу 1 нужно сдвинуть влево на 7 разрядов (в общем случае — на длину ячейки минус 1). Таким образом, итоговая величина сдвига влево определяется как (7 - смещение). | |||
Результирующий код операции установки указанного бита в единицу и основанной на ней операции добавления в множество имеет следующий вид: | |||
void insert(char value) { | |||
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0'); | |||
- | a[index / 8] |= (1 << (7 - index % 8)); | ||
} | |||
=== Установка значения указанного бита в нуль === | |||
Пусть, как и в предыдущем случае, изменяется 20-й бит. Операция установки бита в нуль предполагает, что после её выполнения ячейка массива будет иметь следующий вид: | |||
xxxx0xxx | |||
Обнулить нужный бит, не изменив при этом значения других битов в содержащей его ячейке, можно при помощи побитовой конъюнкции. Маска в этом случае должна будет содержать нуль на месте изменяемого бита и единицы на всех остальных позициях. | |||
xxxxxxxx & | |||
11110111 | |||
= xxxx0xxx | |||
Нетрудно заметить, что искомая маска представляет собой инверсию маски для установки бита в единицу. | Нетрудно заметить, что искомая маска представляет собой инверсию маски для установки бита в единицу. | ||
Код операции установки указанного бита в нуль и основанной на ней операции исключения из множества имеет следующий вид: | Код операции установки указанного бита в нуль и основанной на ней операции исключения из множества имеет следующий вид: | ||
void remove(char value) { | |||
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0'); | |||
a[index / 8] &= ~(1 << (7 - index % 8)); | |||
} | |||
=== Проверка значения указанного бита === | |||
Для того, чтобы выяснить, какое значение (единица или нуль) содержится в указанном бите, можно прибегнуть к следующему приёму. Если обнулить все остальные биты в ячейке, то её значение будет определяться только значением искомого бита: если он содержит нуль, то и вся ячейка также содержит нуль. Обнулить все биты кроме искомого можно с помощью конъюнкции ячейки с маской для установки бита в единицу: | Для того, чтобы выяснить, какое значение (единица или нуль) содержится в указанном бите, можно прибегнуть к следующему приёму. Если обнулить все остальные биты в ячейке, то её значение будет определяться только значением искомого бита: если он содержит нуль, то и вся ячейка также содержит нуль. Обнулить все биты кроме искомого можно с помощью конъюнкции ячейки с маской для установки бита в единицу: | ||
xxxxxxxx & | |||
00001000 | |||
= 0000x000 | |||
Код операции проверки значения указанного бита и основанной на ней операции проверки на вхождение в множество имеет следующий вид: | Код операции проверки значения указанного бита и основанной на ней операции проверки на вхождение в множество имеет следующий вид: | ||
bool contains(char value) { | |||
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0'); | |||
return a[index / 8] & (1 << (7 - index % 8)); | |||
} | |||
---- | |||
Ниже приведён полный код реализации множества на битовом векторе (в предположении, что размер типа <tt>char</tt> равен 1 байт). | |||
class Set { | |||
char a[5]; | |||
public: | |||
Set() { | |||
for (int i = 0; i < 5; i++) | |||
a[i] = 0; | |||
} | |||
void insert(char value) { | |||
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0'); | |||
a[index / 8] |= (1 << (7 - index % 8)); | |||
} | |||
void remove(char value) { | |||
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0'); | |||
a[index / 8] &= ~(1 << (7 - index % 8)); | |||
} | |||
bool contains(char value) { | |||
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0'); | |||
return a[index / 8] & (1 << (7 - index % 8)); | |||
} | |||
}; | |||
Некоторые вопросы для размышления: | |||
*''Каким образом при помощи битовых векторов и битовых операций можно реализовать объединение, пересечение и разность множеств?'' | |||
*''Как может выглядеть реализация битового вектора, позволяющая указывать длину в конструкторе и не зависящая от размеров целочисленных типов на конкретной платформе?'' | |||
== Битовый вектор в STL == | |||
В стандартной библиотеке шаблонов C++ присутствует шаблон [http://www.cplusplus.com/reference/bitset/bitset/ <tt>bitset<N></tt>]. Для возможности его использования требуется подключить заголовочный файл <tt><bitset></tt> и пространство имён <tt>std</tt>: | |||
#include <iostream> | |||
#include <bitset> | |||
using namespace std; | |||
int main() { | |||
bitset<26> b; | |||
char[] s = "example", *p = s; | |||
while (p) | |||
b.set(*p++ - 'a'); | |||
for (char c = 'a', c <= 'z', c++) | |||
if (b.test(c - 'a')) | |||
cout << c << ' '; | |||
return 0; //результат "a e l m p x " | |||
} | |||
STL предоставляет следующий набор методов для битового вектора: | |||
{| class="methodlist" | |||
| || || bitset<N>() || — конструктор битового вектора размера <tt>N</tt>; поддерживается инициализация константой типа <tt>unsigned long</tt> или <tt>string</tt>; | |||
|- | |||
| || bitset<N>& || set(size_t i, bool v = true) || — присвоение биту <tt>i</tt> значения <tt>v</tt>. Вызов без параметров устанавливает значения всех битов в единицы; | |||
|- | |||
| || bitset<N>& || reset(size_t i) || — установка значения бита <tt>i</tt> в нуль. Вызов без параметров устанавливает значения всех битов в нули; | |||
|- | |||
| || bitset<N>& || flip(size_t i) || — инверсия бита <tt>i</tt>. Вызов без параметров инвертирует значения всех битов; | |||
|- | |||
| || bool || test(size_t i) || — проверка значения бита <tt>i</tt>; | |||
|- | |||
| || bool || any() || — проверка на наличие хотя бы одного единичного бита; | |||
|- | |||
| || bool || none() || — проверка на отсутствие единичных битов; | |||
|- | |||
| || size_t || size() || — получение количества битов в векторе; | |||
|- | |||
| || size_t || count() || — получение количества единичных битов в векторе; | |||
|- | |||
| || string || to_string() || — получение представления битового вектора в виде строки; | |||
|- | |||
| || unsigned long || to_ulong() || — получение представления битового вектора в виде значения типа <tt>unsigned long</tt>. Если вектор не умещается в этот тип, возбуждается исключение <tt>overflow_error</tt>. | |||
|} | |||
Кроме этого, для <tt>bitset<N></tt> также определены все битовые операции. Допускается обращение к элементам битового вектора STL (отдельным битам) через квадратные скобки. | |||
bitset<N> | |||
Шаблоны АТД «Множество», представленные в STL, будут рассмотрены в следующих параграфах. | |||
== Ссылки == | |||
Задачи: | |||
* [[:Категория:Задачи: Битовая арифметика|Задачи: Битовая арифметика]] | |||
[[Category:Базовые структуры и абстрактные типы данных]] | |||
Текущая версия от 19:15, 3 марта 2019
Общие сведения
Множество (англ. set) — тип данных, позволяющий хранить ограниченный набор значений и отвечать на вопрос о принадлежности некоторого значения данному набору. Как правило, каждое допустимое значение может входить в множество не более одного раза, хотя возможны исключения, когда множество хранит несколько одинаковых значений (в этом случае для обозначеня АТД применяют термин «мультимножество», англ. multiset).
Интерфейс
Минимальный набор функций, обеспечиваемый множеством, содержит следующие операции:
| void | insert(T value) | — добавление значения value в множество; | |
| void | remove(T value) | — исключение значения value из множества; | |
| bool | contains(T value) | — проверка на вхождение значения value в множество. |
Различные реализации могут также содержать математические операции для множеств (объединение, пересечение и т. д.), поддерживать элементы множества в упорядоченном виде, возвращать количество элементов в множестве (и поддерживать операцию isEmpty()) и т. п.
Демонстрация работы
Реализация на логическом массиве
В тех случаях, когда диапазон значений для множества сравнительно мал, становится возможным определить для каждого допустимого значения отдельную переменную, которая будет указывать на то, содержится ли соответствующее ей значение в множестве. Пусть, например, необходимо реализовать множество строчных латинских символов и десятичных цифр. Так как общее число различных элементов равно 36, для каждого из них можно выделить отдельную логическую переменную. Значение «истина» такой переменной будет свидетельствовать о присутствии соответствующего символа в множестве, значение «ложь» — об его отсутствии.
Работу с большим количеством логических переменных проще организовать, если они представлены в виде массива, но в этом случае необходимо установить взаимно однозначное соответствие между индексами переменных в массиве и значениями в множестве (иными словами, ввести отношение порядка между значениями множества). В нашем примере определим это соответствие следующим образом: пусть нулевой элемент в массиве соответствует символу 'a', первый — символу 'b', ..., 25-й — символу 'z', 26-й — символу '0', 27-й — символу '1', ..., 35-й — символу '9'. В предположении, что в выбранной кодировке символы латинского алфавита и цифры расположены последовательно, мы получаем правило определения переменной, соответствующей символу ch: эта переменная имеет индекс (ch - 'a'), если ch является буквой, либо (26 + ch - '0'), если ch является цифрой.
Вышеприведённые соображения позволяют реализовать множество строчных латинских символов следующим образом:
class Set {
bool a[36];
public:
Set() {
for (int i = 0; i < 36; i++)
a[i] = false;
}
void insert(char value) {
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0');
a[index] = true;
}
void remove(char value) {
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0');
a[index] = false;
}
bool contains(char value) {
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0');
return a[index];
}
};
Однако данная реализация имеет существенный недостаток: так как sizeof(bool) ≥ sizeof(char), массив логических переменных занимает не менее 36 байт = 288 бит, тогда как каждая переменная несёт 1 бит информации, так что весь массив требует 36 бит.
Реализация на битовом векторе
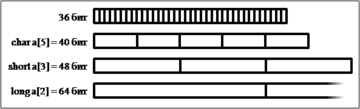
Добиться сокращения объёма используемой памяти можно за счёт манипуляций непосредственно с битами. В этом случае для представления рассмотренного выше множества понадобится 36 бит. Существует несколько возможностей выделить в памяти последовательный блок такого размера:
- Представление переменными типа char даёт массив из 5 элементов, при этом (8 * 5 - 36 = 4) бита будут неиспользуемыми;
- Представление переменными типа short даёт массив из 3 элементов, при этом (16 * 3 - 36 = 12) бит будут неиспользуемыми;
- Представление переменными типа long даёт массив из 2 элементов, при этом (32 * 2 - 36 = 28) бит будут неиспользуемыми.
Минимальный размер памяти, адресуемый с помощью переменной в языке C++, ограничен размером типа char. Поэтому при реализации битовой последовательности, длина которой не кратна sizeof(char), неизбежно появление избыточных битов; их количество тем меньше, чем меньше размер используемого типа данных.
Подобные структуры данных, обеспечивающие использование определённого количества битов в качестве самостоятельных логических переменных, часто называют битовыми массивами или битовыми векторами (англ. bit vector).
Для изменения некоторого бита в битовом векторе требуется соответствующим образом модифицировать элемент массива, содержащий этот бит. Установить, какой ячейке массива принадлежит бит с номером i (нумерация с нуля слева направо), достаточно просто: она будет иметь индекс (i / sizeof(T)), где T — используемый тип элементов. Внутри ячейки искомый бит будет иметь смещение (i % sizeof(T)). Важно, чтобы все остальные биты сохранили свои прежние значения; добиться подобного результата можно с помощью битовых операций языка C++. Битовые операции отличаются от соответствующих логических операций тем, что они применяются последовательно к каждой паре битов значений-операндов, вследствие чего результатом этих операций является новое целочисленное значение. Логические и битовые операции языка C++ описаны в следующей таблице.
| NOT (отрицание) | AND (конъюнкция) | OR (дизъюнкция) | XOR (исключающее ИЛИ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Таблица истинности |
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
| Логическая операция в С++ |
// !
bool a1 = true,
r1 = !a1;
//r1 == false
int a2 = 35,
r2 = !a2;
//r2 == 0
|
// &&
bool a1 = true,
b1 = false,
r1 = a1 && b1;
//r1 == false
int a2 = 35,
b2 = 0,
r2 = a2 && b2;
//r2 == 0
|
// ||
bool a1 = true,
b1 = false,
r1 = a1 || b1;
//r1 == true
int a2 = 35,
b2 = 0,
r2 = a2 || b2;
//r2 == 1
|
отсутствует; для логических переменных эквивалентом является!= | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Битовая операция в С++ |
// ~
short a = 123,
r = ~a;
//r == -124
/*
123: 0000000001111011
-124: 1111111110000100
*/
|
// &
short a = 123,
b = 358,
r = a & b;
//r == 98
/*
123: 0000000001111011
358: 0000000101100110
98: 0000000001100010
*/
|
// |
short a = 123,
b = 358,
r = a | b;
//r == 383
/*
123: 0000000001111011
358: 0000000101100110
383: 0000000101111111
*/
|
// ^
short a = 123,
b = 358,
r = a ^ b;
//r == 285
/*
123: 0000000001111011
358: 0000000101100110
285: 0000000100011101
*/
|
Из таблиц истинности битовых операций можно вывести ряд важных утверждений:
- Конъюнкция бита с единичным битом не изменяет его значение;
- Конъюнкция бита с нулевым битом меняет его значение на 0;
- Дизъюнкция бита с единичным битом меняет его значение на 1;
- Дизъюнкция бита с нулевым битом не изменяет его значение.
Установка значения указанного бита в единицу
Здесь и далее будем предполагать, что битовый вектор построен на массиве переменных типа char, размер которого равен 1 байт. Пусть требуется установить значение 20-го бита в единицу (это, например, будет являться признаком вхождения символа 'u' в рассмотренное выше множество). 20-й бит находится в ячейке с индексом (20 / 8 = 2) и имеет смещение (20 % 8 = 4). Эта ячейка в памяти имеет следующий вид:
xxxxxxxx
Здесь x — любое битовое значение (ноль или единица). Значение данной ячейки нужно изменить таким образом, чтобы она приобрела вид
xxxx1xxx
Утверждения, полученные в ходе анализа битовых операций, помогают понять, что для установки значения бита в единицу требуется выполнить побитовую дизъюнкцию содержащей его ячейки со специальным вспомогательным значением, называемым маской. Размер маски должен быть равен размеру ячейки, все биты маски кроме того, который имеет то же смещение, что и модифицируемый бит, должны быть нулевыми, а оставшийся бит — единичным:
xxxxxxxx | 00001000 = xxxx1xxx
Сформировать необходимую для дизъюнкции маску можно, применив к константе 1 (которая имеет битовое представление 00000001) операцию битового сдвига влево (<<). Количество разрядов, на которое осуществляется сдвиг, определяется следующим образом. Единичный бит должен иметь определённое смещение (для 20-го бита равное 4), отсчитываемое от левой границы ячейки. Для того чтобы единичный бит оказался у левой границы ячейки, константу 1 нужно сдвинуть влево на 7 разрядов (в общем случае — на длину ячейки минус 1). Таким образом, итоговая величина сдвига влево определяется как (7 - смещение).
Результирующий код операции установки указанного бита в единицу и основанной на ней операции добавления в множество имеет следующий вид:
void insert(char value) {
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0');
a[index / 8] |= (1 << (7 - index % 8));
}
Установка значения указанного бита в нуль
Пусть, как и в предыдущем случае, изменяется 20-й бит. Операция установки бита в нуль предполагает, что после её выполнения ячейка массива будет иметь следующий вид:
xxxx0xxx
Обнулить нужный бит, не изменив при этом значения других битов в содержащей его ячейке, можно при помощи побитовой конъюнкции. Маска в этом случае должна будет содержать нуль на месте изменяемого бита и единицы на всех остальных позициях.
xxxxxxxx & 11110111 = xxxx0xxx
Нетрудно заметить, что искомая маска представляет собой инверсию маски для установки бита в единицу.
Код операции установки указанного бита в нуль и основанной на ней операции исключения из множества имеет следующий вид:
void remove(char value) {
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0');
a[index / 8] &= ~(1 << (7 - index % 8));
}
Проверка значения указанного бита
Для того, чтобы выяснить, какое значение (единица или нуль) содержится в указанном бите, можно прибегнуть к следующему приёму. Если обнулить все остальные биты в ячейке, то её значение будет определяться только значением искомого бита: если он содержит нуль, то и вся ячейка также содержит нуль. Обнулить все биты кроме искомого можно с помощью конъюнкции ячейки с маской для установки бита в единицу:
xxxxxxxx & 00001000 = 0000x000
Код операции проверки значения указанного бита и основанной на ней операции проверки на вхождение в множество имеет следующий вид:
bool contains(char value) {
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0');
return a[index / 8] & (1 << (7 - index % 8));
}
Ниже приведён полный код реализации множества на битовом векторе (в предположении, что размер типа char равен 1 байт).
class Set {
char a[5];
public:
Set() {
for (int i = 0; i < 5; i++)
a[i] = 0;
}
void insert(char value) {
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0');
a[index / 8] |= (1 << (7 - index % 8));
}
void remove(char value) {
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0');
a[index / 8] &= ~(1 << (7 - index % 8));
}
bool contains(char value) {
int index = (value >= 'a' && value <= 'z' ? value - 'a' : 26 + value - '0');
return a[index / 8] & (1 << (7 - index % 8));
}
};
Некоторые вопросы для размышления:
- Каким образом при помощи битовых векторов и битовых операций можно реализовать объединение, пересечение и разность множеств?
- Как может выглядеть реализация битового вектора, позволяющая указывать длину в конструкторе и не зависящая от размеров целочисленных типов на конкретной платформе?
Битовый вектор в STL
В стандартной библиотеке шаблонов C++ присутствует шаблон bitset<N>. Для возможности его использования требуется подключить заголовочный файл <bitset> и пространство имён std:
#include <iostream>
#include <bitset>
using namespace std;
int main() {
bitset<26> b;
char[] s = "example", *p = s;
while (p)
b.set(*p++ - 'a');
for (char c = 'a', c <= 'z', c++)
if (b.test(c - 'a'))
cout << c << ' ';
return 0; //результат "a e l m p x "
}
STL предоставляет следующий набор методов для битового вектора:
| bitset<N>() | — конструктор битового вектора размера N; поддерживается инициализация константой типа unsigned long или string; | ||
| bitset<N>& | set(size_t i, bool v = true) | — присвоение биту i значения v. Вызов без параметров устанавливает значения всех битов в единицы; | |
| bitset<N>& | reset(size_t i) | — установка значения бита i в нуль. Вызов без параметров устанавливает значения всех битов в нули; | |
| bitset<N>& | flip(size_t i) | — инверсия бита i. Вызов без параметров инвертирует значения всех битов; | |
| bool | test(size_t i) | — проверка значения бита i; | |
| bool | any() | — проверка на наличие хотя бы одного единичного бита; | |
| bool | none() | — проверка на отсутствие единичных битов; | |
| size_t | size() | — получение количества битов в векторе; | |
| size_t | count() | — получение количества единичных битов в векторе; | |
| string | to_string() | — получение представления битового вектора в виде строки; | |
| unsigned long | to_ulong() | — получение представления битового вектора в виде значения типа unsigned long. Если вектор не умещается в этот тип, возбуждается исключение overflow_error. |
Кроме этого, для bitset<N> также определены все битовые операции. Допускается обращение к элементам битового вектора STL (отдельным битам) через квадратные скобки.
Шаблоны АТД «Множество», представленные в STL, будут рассмотрены в следующих параграфах.
Ссылки
Задачи: