Практика ИВТ — 2017: различия между версиями
Ctrlalt (обсуждение | вклад) |
Ctrlalt (обсуждение | вклад) Нет описания правки |
||
| Строка 72: | Строка 72: | ||
== Измерение быстродействия решений == | == Измерение быстродействия решений == | ||
< | === Пример выполнения === | ||
Предположим, что согласно варианту требуется проанализировать быстро действие решения [http://acmp.ru/index.asp?main=task&id_task=122 задачи о наибольшей возрастающей подпоследовательности]. | |||
Допустим, что было составлено и сдано следующее решение (хотя оно далеко не единственное и не самое эффективное из возможных): | |||
#include <stdio.h> | |||
#include <vector> | |||
using namespace std; | |||
vector<int> readArray() { | |||
int aSize; | |||
scanf("%d", &aSize); | |||
vector<int> a(aSize); | |||
for (int i = 0; i < aSize; i++) | |||
scanf("%d", &a[i]); | |||
return a; | |||
} | |||
int lisLength(vector<int> &a) { | |||
vector<int> length(a.size()); | |||
int maxLength = 0; | |||
for (int i = 0; i < a.size(); i++) { | |||
length[i] = 1; | |||
for (int j = 0; j < i; j++) { | |||
if (a[j] < a[i] && length[i] < length[j] + 1) | |||
length[i] = length[j] + 1; | |||
} | |||
if (maxLength < length[i]) | |||
maxLength = length[i]; | |||
} | |||
return maxLength; | |||
} | |||
int main() { | |||
vector<int> a = readArray(); | |||
printf("%d", lisLength(a)); | |||
} | |||
Чтобы проанализировать эффективность программы, необходимо сделать несколько измерений времени её работы, увеличивая размер обрабатываемых входных данных. | |||
Для тестирования прежде всего понадобится генератор случайных входных данных заданного размера. Для рассматриваемой задачи входными данными является целочисленный массив: | |||
#include <stdlib.h> | |||
int random(int l, int r) { | |||
return l + rand() % (r - l + 1); | |||
} | |||
vector<int> generateArray(int size) { | |||
vector<int> a(size); | |||
for (int i = 0; i < size; i++) | |||
a[i] = random(-100, 100); | |||
return a; | |||
} | |||
Теперь можно составить функцию, измеряющее время работы (обратите внимание, что [http://www.cplusplus.com/reference/chrono/|заголовочный файл <chrono>] появился только в стандарте C++11 — вам понадобится относительно современная версия компилятора): | |||
using namespace std::chrono; | |||
double singleTimeTest(int size) { | |||
vector<int> a = generateArray(size); | |||
high_resolution_clock::time_point startTime = high_resolution_clock::now(); | |||
lisLength(a); | |||
high_resolution_clock::time_point finishTime = high_resolution_clock::now(); | |||
duration<double> elapsedTime = duration_cast<duration<double>>(finishTime - startTime); | |||
return elapsedTime.count(); | |||
} | |||
Чтобы исключить влияние вырожденных входных данных на результаты измерений, составим функцию, запускающую тест множество раз и возвращающую среднее время выполнения: | |||
double multipleTimeTests(int size, int testsCount) { | |||
double totalTime = 0; | |||
for (int i = 0; i < testsCount; i++) | |||
totalTime += singleTimeTest(size); | |||
return totalTime / testsCount; | |||
} | |||
Теперь можно составить функцию, выводящую результаты тестирования: | |||
void timeTestingTable() { | |||
printf("N\tT(N)\n"); | |||
for (int n = 16; n <= 8192; n *= 2) | |||
printf("%d\t%lf\n", n, multipleTimeTests(n, 100)); | |||
} | |||
[http://ideone.com/hDwfGb Полный код рассматриваемого примера] | |||
=== Интерпретация результатов === | |||
Пусть после вызова функции <tt>timeTestingTable()</tt> получился следующий вывод: | |||
N T(N) | |||
16 0.000001 | |||
32 0.000004 | |||
64 0.000015 | |||
128 0.000051 | |||
256 0.000168 | |||
512 0.000667 | |||
1024 0.002793 | |||
2048 0.011155 | |||
4096 0.044568 | |||
8192 0.177109 | |||
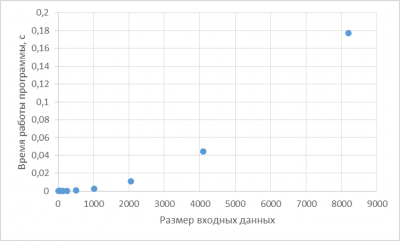
Отметим показанные точки на графике при помощи Excel (не забывайте подписывать оси!). Также можно использовать [http://www.wolframalpha.com/input/?i=ListPlot+%5B%7B16,+0.000001%7D,+%7B32,+0.000004%7D,+%7B64,+0.000015%7D,+%7B128,+0.000051%7D,+%7B256,+0.000168%7D,+%7B512,+0.000667%7D,+%7B1024,+0.002793%7D,+%7B2048,+0.011155%7D,+%7B4096,+0.044568%7D,+%7B8192,+0.177109%7D%5D WolframAlpha] | |||
[[Файл:time1.png|400px]] | |||
В данном случае видно, что с увеличением размера входных данных в 2 раза время работы программы возрастает примерно в 4 раза. Это позволяет сделать предположение о том, что время работы пропорционально квадрату размера входных данных (T(N) ~ N<sup>2</sup>). | |||
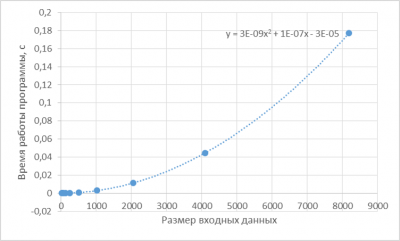
Добавим на график соответствующую линию тренда (тип — полиномиальная степени 2, показывать уравнение на графике). Вновь можно использовать [http://www.wolframalpha.com/input/?i=quadratic+fit+%7B16,+0.000001%7D,+%7B32,+0.000004%7D,+%7B64,+0.000015%7D,+%7B128,+0.000051%7D,+%7B256,+0.000168%7D,+%7B512,+0.000667%7D,+%7B1024,+0.002793%7D,+%7B2048,+0.011155%7D,+%7B4096,+0.044568%7D,+%7B8192,+0.177109%7D WolframAlpha]. Видно, что линия действительно хорошо приближает полученные результаты: | |||
[[Файл:time2.png|400px]] | |||
Составим таблицу оценки погрешностей, чтобы обосновать адекватность приближения: | |||
{| class="standard centered w60px" | |||
|'''N'''||'''T<sub>эксп</sub>(N)'''||'''T<sub>теор</sub>(N)'''||'''Δ'''||'''δ''' | |||
|- | |||
|16||0.000001||-0.000028||0.000029||28.632000 | |||
|- | |||
|32||0.000004||-0.000024||0.000028||6.932000 | |||
|- | |||
|64||0.000015||-0.000011||0.000026||1.754133 | |||
|- | |||
|128||0.000051||0.000032||0.000019||0.373490 | |||
|- | |||
|256||0.000168||0.000192||0.000024||0.144095 | |||
|- | |||
|512||0.000667||0.000808||0.000141||0.210843 | |||
|- | |||
|1024||0.002793||0.003218||0.000425||0.152212 | |||
|- | |||
|2048||0.011155||0.012758||0.001603||0.143677 | |||
|- | |||
|4096||0.044568||0.050711||0.006143||0.137840 | |||
|- | |||
|8192||0.177109||0.202116||0.025007||0.141194 | |||
|} | |||
'''T<sub>теор</sub>(N)''' вычисляется путём подстановки N в уравнение линии тренда. | |||
'''Δ''' — абсолютная погрешность, вычисляется как |T<sub>эксп</sub>(N) - T<sub>теор</sub>(N)|. | |||
'''δ''' — относительная погрешность, вычисляется как δ / T<sub>эксп</sub>(N). Ожидается, что относительная погрешность окажется достаточно малой (для больших N). | |||
Важно: в вашем варианте может оказаться другая закономерность: | |||
* T(N) ~ 1 (точки принадлежат горизонтальной прямой) | |||
* T(N) ~ logN | |||
* T(N) ~ √N (стройте линию тренда для T<sup>2</sup>(N)) | |||
* T(N) ~ N | |||
* T(N) ~ NlogN (стройте линию тренда для T(N) / logN) | |||
* T(N) ~ N<sup>3</sup> | |||
== Тестирование корректности решений == | == Тестирование корректности решений == | ||
(будет добавлено позднее) | |||
== Отчёт по практике == | == Отчёт по практике == | ||
(будет добавлено позднее) | |||
== Критерии оценки == | == Критерии оценки == | ||
Версия от 03:50, 14 июня 2017
В любой непонятной ситуации
сохраняйте спокойствие и пишите на v.folunin@ulstu.ru (не забывайте представиться и написать «Практика ИВТ» в теме письма).
Задание на практику
Обязательная часть:
- Заполнить дневник практики;
- Решить предложенные задачи по программированию на языке C++;
- Измерить быстродействие решения одной задачи (по варианту);
- Составить отчёт по практике.
Для аттестации по практике должны быть выполнены все пункты обязательной части (тем не менее, можно решить не все задачи: см. критерии оценки ниже).
Дополнительная часть:
- Провести тестирование корректности решения одной задачи (по варианту).
Заполнение дневника практики
Титульный лист
- Кафедра «Вычислительная техника»
- Дневник учебной практики
- Студент Иванов Иван Иванович (ваши фамилия, имя и отчество)
- Факультет ФИСТ курс 1
- Группа ИВТАПбд-11 или ИВТВМбд-11 (ваша группа)
- Специальность 09.03.01 Информатика и вычислительная техника (умещайте, можно в 2 строки)
- Ульяновск 2017 г.
Страница 2
- Приказ о назначении на практику №1177 (для ВМ) или 1178 (для АП) от «31» 05 2017 г.
- — вводный от УлГТУ ассистент Фолунин В. А. (оставить место для подписи) «19» 06 2017 г.
- — вводный на предприятии ассистент Фолунин В. А. (оставить место для подписи) «19» 06 2017 г.
- — на рабочем месте ассистент Фолунин В. А. (оставить место для подписи) «19» 06 2017 г.
- Студент Иванов Иван Иванович (ваши фамилия, имя и отчество)
- направлен на учебную практику в
- гор. Ульяновск на УлГТУ
- Срок практики с 19.06.17 по 02.07.17
- Руководитель практики от университета ассистент Фолунин Владимир Александрович
- Прибыл на предприятие "19" 06 2017 г.
- Убыл из предприятия "02" 07 2017 г.
Страница 4
- 19.06.2017 | Инструктаж, УлГТУ
- 20.06.2017 | Решение задач, vtcloud9.ulstu.ru
- 26.06.2017 | Анализ быстродействия решений, vtcloud9.ulstu.ru
- 30.06.2017 | Подготовка отчёта, УлГТУ
Страница 5
- 1) Разработка решений учебных задач по программированию на языке C++
- 2) Проверка корректности решений при помощи автоматизированной тестирующей системы
- 3) Экспериментальное исследование быстродействия решения задачи
- (если вы делаете дополнительную часть) 4) Разработка тестов для анализа корректности решения задачи
Страница 7
- (внизу, под словом Руководитель) 02.07.2017 г.
Страница 8
- (внизу, после места для подписи) 02.07.2017 г.
Решение задач
Откройте сайт тестирующей системы. Слева выберите своё имя из выпадающего списка и введите пароль, выданный преподавателем.
Перейдите на страницу задач практики. Выберите любую задачу. Вы увидите условие, описание формата входных и выходных данных, а также примеры. Вам необходимо разработать консольную программу, которая считывает входные данные с клавиатуры и выводит корректные выходные данные в консоль. При копировании в консоль входных данных примера программа должна выводить результат, в точности совпадающий с показанным в примере, и немедленно завершаться.
В нижней части страницы задачи находится форма отправки решений. В эту форму следует скопировать весь исходный код программы, после чего выбрать компилятор C++ и нажать кнопку «Отправить». Решение будет проверено на большом наборе тестов, результат будет показан сразу после проверки. Программа должна выдавать корректные результаты на всех тестах.
Задачи можно решать в любом порядке. Количество попыток не ограничено.
Настоятельно рекомендуется прочитать руководство для начинающих перед началом работы.
Измерение быстродействия решений
Пример выполнения
Предположим, что согласно варианту требуется проанализировать быстро действие решения задачи о наибольшей возрастающей подпоследовательности.
Допустим, что было составлено и сдано следующее решение (хотя оно далеко не единственное и не самое эффективное из возможных):
#include <stdio.h>
#include <vector>
using namespace std;
vector<int> readArray() {
int aSize;
scanf("%d", &aSize);
vector<int> a(aSize);
for (int i = 0; i < aSize; i++)
scanf("%d", &a[i]);
return a;
}
int lisLength(vector<int> &a) {
vector<int> length(a.size());
int maxLength = 0;
for (int i = 0; i < a.size(); i++) {
length[i] = 1;
for (int j = 0; j < i; j++) {
if (a[j] < a[i] && length[i] < length[j] + 1)
length[i] = length[j] + 1;
}
if (maxLength < length[i])
maxLength = length[i];
}
return maxLength;
}
int main() {
vector<int> a = readArray();
printf("%d", lisLength(a));
}
Чтобы проанализировать эффективность программы, необходимо сделать несколько измерений времени её работы, увеличивая размер обрабатываемых входных данных.
Для тестирования прежде всего понадобится генератор случайных входных данных заданного размера. Для рассматриваемой задачи входными данными является целочисленный массив:
#include <stdlib.h>
int random(int l, int r) {
return l + rand() % (r - l + 1);
}
vector<int> generateArray(int size) {
vector<int> a(size);
for (int i = 0; i < size; i++)
a[i] = random(-100, 100);
return a;
}
Теперь можно составить функцию, измеряющее время работы (обратите внимание, что файл <chrono> появился только в стандарте C++11 — вам понадобится относительно современная версия компилятора):
using namespace std::chrono;
double singleTimeTest(int size) {
vector<int> a = generateArray(size);
high_resolution_clock::time_point startTime = high_resolution_clock::now();
lisLength(a);
high_resolution_clock::time_point finishTime = high_resolution_clock::now();
duration<double> elapsedTime = duration_cast<duration<double>>(finishTime - startTime);
return elapsedTime.count();
}
Чтобы исключить влияние вырожденных входных данных на результаты измерений, составим функцию, запускающую тест множество раз и возвращающую среднее время выполнения:
double multipleTimeTests(int size, int testsCount) {
double totalTime = 0;
for (int i = 0; i < testsCount; i++)
totalTime += singleTimeTest(size);
return totalTime / testsCount;
}
Теперь можно составить функцию, выводящую результаты тестирования:
void timeTestingTable() {
printf("N\tT(N)\n");
for (int n = 16; n <= 8192; n *= 2)
printf("%d\t%lf\n", n, multipleTimeTests(n, 100));
}
Полный код рассматриваемого примера
Интерпретация результатов
Пусть после вызова функции timeTestingTable() получился следующий вывод:
N T(N) 16 0.000001 32 0.000004 64 0.000015 128 0.000051 256 0.000168 512 0.000667 1024 0.002793 2048 0.011155 4096 0.044568 8192 0.177109
Отметим показанные точки на графике при помощи Excel (не забывайте подписывать оси!). Также можно использовать WolframAlpha
В данном случае видно, что с увеличением размера входных данных в 2 раза время работы программы возрастает примерно в 4 раза. Это позволяет сделать предположение о том, что время работы пропорционально квадрату размера входных данных (T(N) ~ N2).
Добавим на график соответствующую линию тренда (тип — полиномиальная степени 2, показывать уравнение на графике). Вновь можно использовать WolframAlpha. Видно, что линия действительно хорошо приближает полученные результаты:
Составим таблицу оценки погрешностей, чтобы обосновать адекватность приближения:
| N | Tэксп(N) | Tтеор(N) | Δ | δ |
| 16 | 0.000001 | -0.000028 | 0.000029 | 28.632000 |
| 32 | 0.000004 | -0.000024 | 0.000028 | 6.932000 |
| 64 | 0.000015 | -0.000011 | 0.000026 | 1.754133 |
| 128 | 0.000051 | 0.000032 | 0.000019 | 0.373490 |
| 256 | 0.000168 | 0.000192 | 0.000024 | 0.144095 |
| 512 | 0.000667 | 0.000808 | 0.000141 | 0.210843 |
| 1024 | 0.002793 | 0.003218 | 0.000425 | 0.152212 |
| 2048 | 0.011155 | 0.012758 | 0.001603 | 0.143677 |
| 4096 | 0.044568 | 0.050711 | 0.006143 | 0.137840 |
| 8192 | 0.177109 | 0.202116 | 0.025007 | 0.141194 |
Tтеор(N) вычисляется путём подстановки N в уравнение линии тренда.
Δ — абсолютная погрешность, вычисляется как |Tэксп(N) - Tтеор(N)|.
δ — относительная погрешность, вычисляется как δ / Tэксп(N). Ожидается, что относительная погрешность окажется достаточно малой (для больших N).
Важно: в вашем варианте может оказаться другая закономерность:
- T(N) ~ 1 (точки принадлежат горизонтальной прямой)
- T(N) ~ logN
- T(N) ~ √N (стройте линию тренда для T2(N))
- T(N) ~ N
- T(N) ~ NlogN (стройте линию тренда для T(N) / logN)
- T(N) ~ N3
Тестирование корректности решений
(будет добавлено позднее)
Отчёт по практике
(будет добавлено позднее)
Критерии оценки
- Заполнение дневника — 20 баллов;
- Составление отчёта — 20 баллов;
- Решение задачи — 2 балла за каждую задачу;
- Отсутствие ошибок форматирования в решении — +1 балл за каждую задачу (эта часть будет проверяться очень дотошно — два пробела не на своём месте, и балл не добавляется);
- Наличие глобальных переменных в решении — -1 балл за каждую задачу;
- Плагиат — -15 баллов за каждую задачу (и у того, кто заимствовал решение, и у того, кто одолжил решение);
- Измерение быстродействия решения — 25 баллов;
- Тестирование корректности решения — 25 баллов.
100 баллов — оценка «Удовлетворительно»
200 баллов — оценка «Хорошо»
300 баллов — оценка «Отлично»