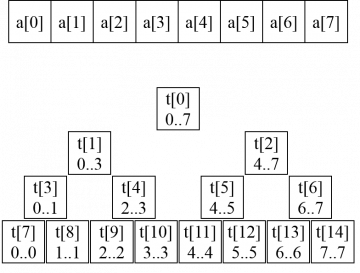
Дерево отрезков
Запрос на отрезке и модификация отдельных элементов
- Если отрезок текущей вершины не пересекается с отрезком запроса, то возвращается нейтральное значение.
- Если отрезок текущей вершины целиком включён в отрезок запроса, то возвращается значение, хранящееся в текущей вершине.
- Во всех остальных случаях запрос перенаправляется потомкам текущей вершины.
Можно выделить два распространённых способа реализации данной логики:
if (r < vl || vr < l)
//отрезки не пересекаются
if (l <= vl && vr <= r)
//отрезок текущей вершины принадлежит отрезку запроса
query(2 * v + 1, vl, vm, l, r);
query(2 * v + 2, vm + 1, vr, l, r);
|
if (l > r)
//отрезки не пересекаются
if (l == vl && vr == r)
//отрезок текущей вершины принадлежит отрезку запроса
query(2 * v + 1, vl, vm, l, min(r, vm));
query(2 * v + 2, vm + 1, vr, max(l, vm + 1), r);
|
int t[4 * 100010];
void build(int v, int vl, int vr, int a[]) {
if (vl == vr) {
t[v] = a[vl];
return;
}
int vm = vl + (vr - vl) / 2;
build(2 * v + 1, vl, vm, a);
build(2 * v + 2, vm + 1, vr, a);
t[v] = t[2 * v + 1] + t[2 * v + 2];
}
int query(int v, int vl, int vr, int l, int r) {
if (r < vl || vr < l)
return 0;
if (l <= vl && vr <= r)
return t[v];
int vm = vl + (vr - vl) / 2;
int ql = query(2 * v + 1, vl, vm, l, r);
int qr = query(2 * v + 2, vm + 1, vr, l, r);
return ql + qr;
}
void modify(int v, int vl, int vr, int pos, int val) {
if (pos < vl || vr < pos)
return;
if (pos == vl && vl == vr) {
t[v] += val;
return;
}
int vm = vl + (vr - vl) / 2;
modify(2 * v + 1, vl, vm, pos, val);
modify(2 * v + 2, vm + 1, vr, pos, val);
t[v] = t[2 * v + 1] + t[2 * v + 2];
}
Запрос на отрезке и модификация на отрезке
- Считаем, что актуальное значение в вершине v равно t[v] + add[v] * (vr - vl + 1).
- Перед выводом результата или передачей запроса будем спускать значение add[v] потомкам текущей вершины при помощи функции push().
int t[4 * 100010], add[4 * 100010];
void push(int v, int vl, int vr) {
if (vl != vr) {
add[2 * v + 1] += add[v];
add[2 * v + 2] += add[v];
}
t[v] += add[v] * (vr - vl + 1);
add[v] = 0;
}
void build(int v, int vl, int vr, int a[]) {
if (vl == vr) {
t[v] = a[vl];
return;
}
int vm = vl + (vr - vl) / 2;
build(2 * v + 1, vl, vm, a);
build(2 * v + 2, vm + 1, vr, a);
t[v] = t[2 * v + 1] + t[2 * v + 2];
}
int query(int v, int vl, int vr, int l, int r) {
push(v, vl, vr);
if (r < vl || vr < l)
return 0;
if (l <= vl && vr <= r)
return t[v];
int vm = vl + (vr - vl) / 2;
int ql = query(2 * v + 1, vl, vm, l, r);
int qr = query(2 * v + 2, vm + 1, vr, l, r);
return ql + qr;
}
void modify(int v, int vl, int vr, int l, int r, int val) {
push(v, vl, vr);
if (r < vl || vr < l)
return;
if (l <= vl && vr <= r) {
add[v] += val;
push(v, vl, vr);
return;
}
int vm = vl + (vr - vl) / 2;
modify(2 * v + 1, vl, vm, l, r, val);
modify(2 * v + 2, vm + 1, vr, l, r, val);
t[v] = t[2 * v + 1] + t[2 * v + 2];
}
Почему для хранения дерева отрезков требуется массив размера 4n?
Пусть для массива a[] из n элементов создаётся дерево отрезков, хранящееся в массиве t[]. Правило требует, чтобы размер массива t[] был не менее 4n.
Однако можно рассуждать следующим образом: двоичным деревом с наибольшим количеством элементов является полное двоичное дерево. Если количество листьев в полном двоичном дереве равно n, то общее количество вершин в нём равно 2n - 1. Возможно ли, что для хранения дерева отрезков всегда будет достаточно массива размера 2n?
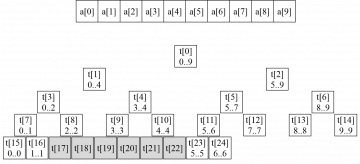
К сожалению, это не так. Процедура build не обязательно формирует полное двоичное дерево; некоторые элементы массива t[] могут не использоваться. Например, если n = 5, то дерево отрезков имеет высоту 4 и содержит 9 элементов. Если N = 10, объединяются два таких дерева высоты 4, и на нижнем уровне появляются 6 неиспользуемых элементов (t[17]..t[22]).
Оценим более точно требуемый размер массива t[].
Прежде всего определим вспомогательные функции leftHalf(n) и rightHalf(n), возвращающие размер левого и правого поддеревьев дерева отрезков для массива a[] из n элементов (n > 1). Если n чётно, то обе функции возвращают n / 2. Если n нечётно, то средний элемент относится к левой части.
int leftHalf(int n) {
return n / 2 + n % 2;
}
int rightHalf(int n) {
return n / 2;
}
Далее определим функцию height(n), возвращающую высоту дерева отрезков для массива a[] из n элементов. Если n = 1, то height(n) = 1. В других случаях height(n) = 1 + max(height(leftHalf(n)), height(rightHalf(n))); так как левое поддерево всегда не меньше правого, эту запись можно упростить: height(n) = 1 + height(leftHalf(n)).
Кроме того, определим функцию fullSize(h), возвращающую размер полного двоичного дерева высоты h.
int height(int n) {
if (n == 1)
return 1;
else
return 1 + height(leftHalf(n));
}
int fullSize(int h) {
return (1 << h) - 1;
}
Наконец, определим функцию tSize(n), возвращающую размер t[] для массива a[] из n элементов. Если n = 1, то tSize(n) = 1. Далее, если левое и правое поддерево имеют одинаковую высоту, то необходимый размер t[] определяется последним (нижним) элементом правого поддерева, а левое поддерево становится полным: tSize(n) = 1 + fullSize(height(leftHalf(n))) + tSize(rightHalf(n)). Если же левое поддерево выше правого, то необходимый размер t[] определяется последним (нижним) элементом левого поддерева, а правое поддерево становится полным: tSize(n) = 1 + tSize(leftHalf(n)) + fullSize(height(rightHalf(n))).
int tSize(int n) {
if (n == 1)
return 1;
int leftHeight = height(leftHalf(n)), rightHeight = height(rightHalf(n));
if (leftHeight == rightHeight)
return 1 + fullSize(leftHeight) + tSize(rightHalf(n));
else
return 1 + tSize(leftHalf(n)) + fullSize(rightHeight);
}
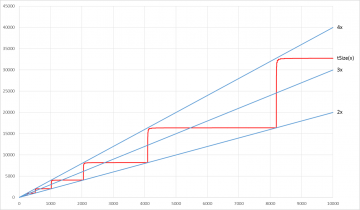
Можно видеть, что график функции tSize практически всегда находится выше графика функции 2x и всегда ниже графика функции 4x. Например, tSize(8448) = 32705, что значительно превышает не только удвоенный, но и утроенный размер исходного массива.
Ссылки
Теория:
- e-maxx.ru — Дерево отрезков
- neerc.ifmo.ru/wiki — Дерево отрезков
- brestprog.neocities.org — Дерево отрезков
Демонстрация:
Код:
Задачи: