Алгоритм Дейкстры

Материал из Олимпиадное программирование в УлГТУ
Перейти к навигации Перейти к поиску

Общие сведения

Дан ориентированный или неориентированный взвешенный граф; веса всех рёбер неотрицательны. Требуется определить кратчайшие расстояния из данной вершины до всех остальных.

Пусть изначально расстояние до стартовой вершины равно нулю, расстояния до всех остальных вершин — бесконечности. Определим ближайшую вершину (на первом шаге таковой будет стартовая вершина). Как будет показано ниже, расстояние до выбранной вершины является кратчайшим и в дальнейшем не изменяется, поэтому его можно использовать для пересчёта расстояний до соседних вершин.

Итак, пусть v — текущая ближайшая вершина и существует ребро v → to веса w. Обозначим кратчайшее расстояние до вершины v как dist[v], текущее расстояние до вершины to — dist[to]. Тогда если (dist[v] + w) < dist[to], то мы нашли более короткий путь к вершине to — он проходит через вершину v и ребро v → to. Следовательно, мы можем обновить значение dist[to]. Такое обновление называется релаксацией.

После проведения всех возможных релаксаций ближайшая вершина исключается из дальнейшего рассмотрения. Таким образом, на каждой итерации будет определяться кратчайшее расстояние до одной из вершин графа, и всего для решения задачи понадобится V итераций. Очевидно, что после выполнения алгоритма расстояния до недостижимых вершин останутся равными бесконечности.

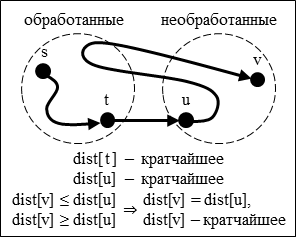
Доказательство корректности алгоритма Дейкстры

Доказательство того факта, что на каждой итерации расстояние до обрабатываемой вершины действительно является кратчайшим, проводится по индукции. Для базового случая (обрабатывается стартовая вершина, расстояние до неё равно нулю) утверждение выполняется. Далее, пусть утверждение выполняется для всех обработанных вершин (значения dist[] для них рассчитаны верно), а на текущем шаге выбрана вершина v. Обозначим через u первую необработанную вершину на кратчайшем пути до v, через t — вершину, предшествующую u на этом пути. Кратчайшее расстояние до вершины u равно сумме dist[t] и веса ребра t → u; эта сумма уже была записана в dist[u] при проведении релаксаций из вершины t, следовательно, значение dist[u] действительно равно кратчайшему расстоянию до вершины u. Далее, заметим, что должны выполняться условия dist[v] ≤ dist[u] (так как вершина v является ближайшей на текущем шаге) и dist[v] ≥ dist[u] (так как u лежит на пути до v, а граф не содержит рёбер отрицательного веса). Отсюда dist[v] = dist[u], то есть в момент выбора вершины v значение dist[v] действительно равно кратчайшему расстоянию до неё.

Демонстрация работы

Реализация для плотных графов

Здесь и далее будем считать, что граф задан списками смежности, а количество вершин равно n. 

struct Edge {
    int from, to;
    int weight;
};
vector<vector<Edge>> g(n);

Алгоритм принимает индекс стартовой вершины vStart и заполняет глобальный массив dist[]. Роль значения «бесконечность» выполняет достаточно большая константа INF; её значение должно быть больше максимального возможного расстояния между вершинами, но не допускать переполнения при проведении релаксаций (для избежания переполнений также можно ввести в основной цикл контрольное условие: если расстояние до ближайшей вершины равно INF, выполнение алгоритма завершается). Логический массив visited[] предназначен для отметки обработанных вершин.

После начальной инициализации visited[] и dist[] производится n итераций алгоритма, на каждой из которых сначала определяется ближайшая из необработанных вершин (используется наивный поиск минимума с асимптотикой O(V)), затем выбранная вершина помечается как обработанная и производится попытка релаксации для каждого исходящего из неё ребра.

Хотя на каждой итерации выполняется различное число попыток релаксации, общее их количество равно E, так как будет просмотрено каждое ребро (один раз, если рёбра направленные, дважды — если ненаправленные). Таким образом, общая асимптотическая оценка алгоритма равна O(V2 + E). 

vector<bool> visited(n);
vector<int> dist(n);
const int INF = 1e9;

void dijkstra(int vStart) {
    fill(visited.begin(), visited.end(), 0);
    fill(dist.begin(), dist.end(), INF);
    dist[vStart] = 0;
    
    for (int i = 0; i < n; i++) {
        int nearestV = -1;
        for (int v = 0; v < n; v++)
            if (!visited[v] && (nearestV == -1 || dist[v] < dist[nearestV]))
                nearestV = v;

        visited[nearestV] = true;

        for (Edge &e : g[nearestV]) {
            int to = e.to, w = e.weight;
            if (dist[to] > dist[nearestV] + w)
                dist[to] = dist[nearestV] + w;
        }              
    }
}

Реализация для разреженных графов

Алгоритм Дейкстры выполняет O(V) поисков ближайшей вершины и O(E) релаксаций. В предыдущей реализации информация о расстоянии до вершин хранилась в массиве, что позволяло производить операции первого типа за O(V), второго типа — за O(1). Итоговая оценка O(V2 + E) является неудовлетворительной для разреженных графов (в которых E << V2). Поэтому в данном случае имеет смысл использовать структуры данных, позволяющие производить и поиск минимума, и обновление элементов с асимптотикой O(logV).

Одной из таких структур является сбалансированное двоичное дерево поиска, представленное в STL контейнером set. Так как требуется упорядочить вершины согласно расстоянию до них, будем хранить множество s из пар (расстояние, индекс вершины). Пары STL сравниваются начиная с первого поля, что обеспечит нужный порядок. Множество s также будет выполнять функции массива used[], так как в него будут помещаться только необработанные вершины.

Теперь для определения ближайшей вершины достаточно обратиться к полю s.begin(). При проведении релаксации нужно предварительно удалить из множества пару со старым расстоянием (если она там была), а затем добавить пару с обновлённым расстоянием.

Итоговая асимптотика данной реализации составляет O((V + E)logV), что в большинстве случаев сводится к O(ElogV). Следует обратить внимание на то, что для плотных графов (в которых E ≈ V2) эта реализация оказывается медленнее предыдущей. 

set<pair<int, int>> s;
vector<int> dist(n);
const int INF = 1e9;

void dijkstra(int vStart) {
    fill(dist.begin(), dist.end(), INF);
    dist[vStart] = 0;
    s.insert({ dist[vStart], vStart });
    
    while (!s.empty()) {
        int nearestV = s.begin()->second;
        s.erase(s.begin());

        for (Edge &e : g[nearestV]) {
            int to = e.to, w = e.weight;
            if (dist[to] > dist[nearestV] + w) {
                s.erase({ dist[to], to });
                dist[to] = dist[nearestV] + w;
                s.insert({ dist[to], to });
            }
        }              
    }
}

Восстановление путей

Если в задаче требуется выводить сами кратчайшие пути, то нужно поддерживать массив предков parent[]: ячейка parent[v] содержит индекс непосредственного предка вершины v на кратчайшем пути от стартовой вершины до v. Изначально предок каждой вершины не определён, что помечается значением -1; обновление предка происходит вместе с обновлением кратчайшего расстояния при успешной релаксации.

После завершения работы алгоритма можно восстановить кратчайший путь от начальной вершины до некоторой достижимой вершины vFinish в обратном порядке, последовательно перемещаясь по массиву parent[], пока текущая вершина не станет равной -1. В конце нужно развернуть получившуюся последовательность вершин. 

vector<int> parent(n, -1);

if (dist[to] > dist[nearestV] + w) {             
    dist[to] = dist[nearestV] + w;
    parent[to] = nearestV;          
}
  
vector<int> path;

for (int v = vFinish; v != -1; v = parent[v])
     path.push_back(v);
 
reverse(path.begin(), path.end());

Если в графе присутствуют кратные рёбра между одной и той же парой вершин, то логику определения кратчайшего пути придётся усложнить. В данных условиях можно явно сохранить все рёбра графа в отдельном массиве, а в массив parent[] записывать индекс того ребра, по которому осуществлялась релаксация. При этом можно изменить представление графа: вместо хранения списка смежных рёбер для каждой вершины (vector<vector<Edge>> g) можно хранить список индексов этих рёбер в массиве рёбер (vector<vector<int>> g).

Ссылки на задачи

Ссылки

Источник — https://acm.khpnets.info/w39/index.php?title=Алгоритм_Дейкстры&oldid=2505