Алгоритм Дейкстры

Общие сведения

Дан ориентированный или неориентированный взвешенный граф; веса всех рёбер неотрицательны. Требуется определить кратчайшие расстояния из данной вершины до всех остальных.

Пусть изначально расстояние до стартовой вершины равно нулю, расстояния до всех остальных вершин — бесконечности. Определим ближайшую вершину (на первом шаге таковой будет стартовая вершина). Как будет показано ниже, расстояние до выбранной вершины является кратчайшим и в дальнейшем не изменяется, поэтому его можно использовать для пересчёта расстояний до соседних вершин.

Итак, пусть v — текущая ближайшая вершина и существует ребро v→u веса w. Обозначим кратчайшее расстояние до вершины v как dist[v], текущее расстояние до вершины u — dist[u]. Тогда если (dist[v] + w) < dist[u], то мы нашли более короткий путь к вершине u — он проходит через вершину v и ребро v→u. Соответственно, мы можем обновить значение dist[u]. Такое обновление называется релаксацией.

После проведения всех возможных релаксаций ближайшая вершина исключается из дальнейшего рассмотрения. Таким образом, на каждой итерации будет определяться кратчайшее расстояние до одной из вершин графа, и всего для решения задачи понадобится V итераций. Очевидно, что после выполнения алгоритма расстояния до недостижимых вершин останутся равными бесконечности.

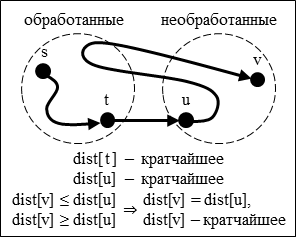
Доказательство корректности алгоритма Дейкстры

Доказательство того факта, что на каждой итерации расстояние до обрабатываемой вершины действительно является кратчайшим, проводится по индукции. Для базового случая (обрабатывается стартовая вершина, расстояние до неё равно нулю) утверждение выполняется. Далее, пусть утверждение выполняется для всех обработанных вершин (значения dist[] для них рассчитаны верно), а на текущем шаге выбрана вершина v. Обозначим через u первую необработанную вершину на кратчайшем пути до v, через t — вершину, предшествующую u на этом пути. Кратчайшее расстояние до вершины u равно сумме dist[t] и веса ребра t→u; эта сумма уже была записана в dist[u] при проведении релаксаций из вершины t, следовательно, значение dist[u] действительно равно кратчайшему расстоянию до вершины u. Далее, заметим, что должны выполняться условия dist[v] ≤ dist[u] (так как вершина v является ближайшей на текущем шаге) и dist[v] ≥ dist[u] (так как u лежит на пути до v, а граф не содержит рёбер отрицательного веса). Отсюда dist[v] = dist[u], то есть в момент выбора вершины v значение dist[v] действительно равно кратчайшему расстоянию до неё.

Демонстрация работы

• Алгоритм Дейкстры

Реализация для плотных графов

Здесь и далее будем считать, что граф задан списками смежности, а количество вершин равно N.

const int N = 1000;
  
struct Edge {
    int vFrom, vTo;
    int weight;
};
vector<Edge> g[N];

const int INF = 1 << 30;
int dist[N];
bool used[N];

void dijkstra(int vStart) {
    for (int i = 0; i < N; i++) {
        used[i] = false;
        dist[i] = INF;
    }
    dist[vStart] = 0;
    
    for (int i = 0; i < N; i++) {
        int v = -1;
        for (int j = 0; j < N; j++)
            if (!used[j] && (v == -1 || dist[j] < dist[v]))
                v = j;
        used[v] = true;
        for (int j = 0; j < g[v].size(); j++) {
            int u = g[v][j].vTo;
            int w = g[v][j].weight;
            if (dist[u] > dist[v] + w)
                dist[u] = dist[v] + w;
        }              
    }
}