Очередь
TLDR
Общие сведения
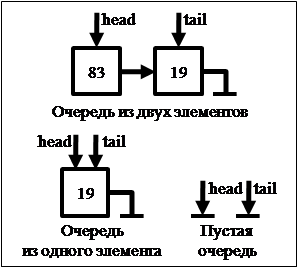
Очередь (англ. queue) — абстрактный контейнер, доступ к элементам которого организован по принципу «первым вошёл — первым вышел» (англ. FIFO, First In — First Out). Поведение элементов очереди напоминает обслуживание покупателей в магазине: каждый новый клиент встаёт в конец очереди и ожидает, когда уйдут все стоящие перед ним.
Для очереди вводятся два абстрактных понятия: хвост (конец) очереди — место, в которое происходит добавление элементов, и голова (начало) очереди — место, из которого происходит удаление элементов.
Интерфейс
Очередь предоставляет три основные операции:
| void | enqueue(T value) | — вставка элемента value в очередь; | |
| T | dequeue() | — извлечение элемента из очереди; | |
| bool | isEmpty() | — проверка очереди на отсутствие элементов. |
Все три метода должны иметь константное время работы (O(1)).
Демонстрация работы
- Data Structure Visualizations — Queue (Linked List Implementation)
- Data Structure Visualizations — Queue (Array Implementation)
- VisuAlgo — Linked List, Stack, Queue, Deque
Реализация на списке
Очередь можно реализовать на односвязном списке. Добавлять элементы в равной степени удобно как в начало списка, так и в конец (если имеется указатель на последний элемент), но в то же время удаление из конца списка реализуется сложнее, чем из начала (так как нужно иметь указатель на предпоследний элемент). Поэтому голова очереди будет располагаться в начале списка, а конец — в конце списка. На голову ссылается указатель Node *head, на хвост — Node *tail.
struct Node {
int val;
Node *next;
Node(int v = 0, Node *n = NULL) {
val = v;
next = n;
}
} *head, *tail;
В конструкторе очереди указатели на голову и хвост инициализируются значением NULL.
Queue() {
head = tail = NULL;
}
Проверка на пустоту
Если очередь не пуста, то указатели head и tail обязательно будут ссылаться на какие-то её элементы (возможно, что на один и тот же). Поэтому проверку на остутствие элементов в очереди можно производить с помощью любого из этих двух указателей:
bool isEmpty() {
return head == NULL;
}
Вставка элемента
Если до вставки элемента очередь пуста, то необходимо выполнить следующие операции:
- Определение нового элемента списка и инициализация его поля val;
- Так как единственный элемент будет являться и началом, и концом очереди, нужно направить на только что созданный элемент указатели head и tail.
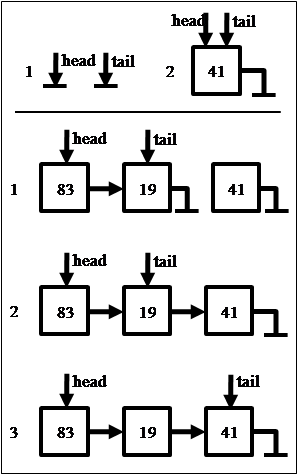
Во всех остальных случаях добавление нового элемента подразумевает следующие действия:
- Определение нового элемента списка и инициализация его поля val;
- Новый элемент будет следовать за текущим конечным, поэтому на него будет указывать поле tail->next;
- Так как новый элемент становится последним, на него теперь будет указывать tail.
Обратите внимание, как выполнение последних двух операций происходит с помощью цепочки присваиваний: сначала адрес нового элемента сохраняется в tail->next, а затем он же передаётся в сам tail.
void enqueue(int value) {
if (head == NULL)
head = tail = new Node(value, NULL);
else
tail = tail->next = new Node(value, NULL);
}
Извлечение элемента
Из пустой очереди нельзя удалить элемент, поэтому, как и в случае стека, такую ситуацию необходимо обрабатывать отдельно.
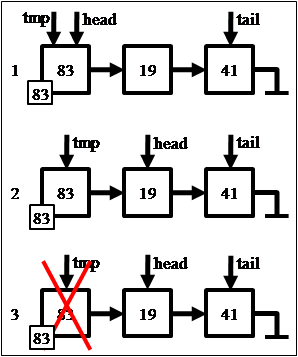
Так как извлечение элемента происходит из начала списка, его реализация для очереди практически повторяет таковую для стека. В обоих случаях удаление предусматривает следующие действия:
- Требуется сохранить значение head->val во временной переменой для возможности последующего возврата;
- Указатель на голову очереди нужно сместить на следующий элемент, но перед этим нужно сохранить во временной переменной предыдущий адрес, чтобы можно было освободить память;
- Единственная разница в реализации заключается в том, что если очередь становится пустой, то требуется явно присвоить значение NULL указателю tail;
- Далее можно освободить память и вернуть сохранённое ранее значение.
int dequeue() {
if (head == NULL)
/* обработка ошибки - нет элементов для извлечения */
int v = head->val;
Node *tmp = head;
head = head->next;
if (head == NULL)
tail = NULL;
delete tmp;
return v;
}
Ниже приведён полный код реализации очереди на односвязном списке. Попытка извлечения из пустой очереди выявляется с помощью конструкции assert (заголовочный файл <assert.h> либо <cassert>).
class Queue {
struct Node {
int val;
Node *next;
Node(int v = 0, Node *n = NULL) {
val = v;
next = n;
}
} *head, *tail;
public:
Queue() {
head = tail = NULL;
}
void enqueue(int value) {
if (head == NULL)
head = tail = new Node(value, NULL);
else
tail = tail->next = new Node(value, NULL);
}
int dequeue() {
assert(head != NULL);
int v = head->val;
Node *tmp = head;
head = head->next;
if (head == NULL)
tail = NULL;
delete tmp;
return v;
}
bool isEmpty() {
return head == NULL;
}
};
Реализация на массиве
Как и стек, очередь может быть реализована на массивах, и ограничения такой реализации те же: фиксированный максимальный размер очереди и потребление памяти, не зависящее от количества элементов в очереди.
static const int MAX_SIZE = 100;
int a[MAX_SIZE];
int head, tail;
Queue() {
head = tail = 0;
}
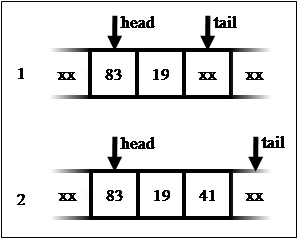
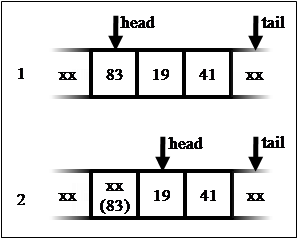
При реализации очереди на массиве определяются два индекса head и tail. При добавлении элемента он сохраняется в ячейку массива, на которую указывает tail, и затем tail смещается далее по массиву. При удалении элемента сдвигается уже индекс head, причём в том же направлении (смещение самих хранящихся элементов к началу массива невозможно по причине сложности O(N)).
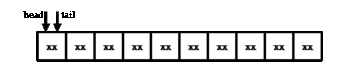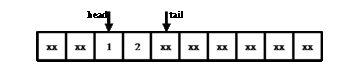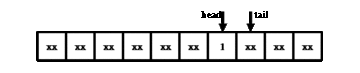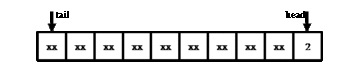
Получается ситуация, в которой область, содержащая хранящиеся в очереди элементы, непрерывно смещается в сторону конца массива. Решением этой проблемы является «зацикливание» очереди, когда все смещения индексов происходят по модулю длины массива. Тогда после достижения конца массива область хранения элементов продолжается в начале массива.
На иллюстрации показана работа очереди на массиве из 10 элементов. Производится бесконечный цикл из двух операций вставки и двух операций извлечения. Символом «xx» обозначены ячейки массива, которые в текущий момент не хранят элементы очереди (и фактические значения которых нам в данный момент безразличны).
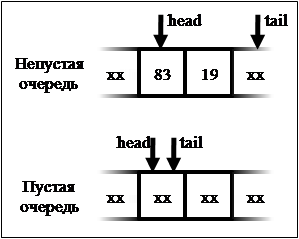
Проверка на пустоту
Можно видеть, что в том случае, когда очередь не содержит элементов, индексы head и tail указывают на одну и ту же ячейку.
bool isEmpty() {
return head == tail;
}
Вставка элемента
Новый элемент вставляется в то место, на которое указывает индекс tail. Сам индекс после вставки необходимо увеличить (по модулю длины массива, чтобы обеспечить цикличность). Нужно отслеживать переполнение очереди, признаком которого будет являться равенство значений head и tail после увеличения.
void push(int value) {
if ((tail + 1) % MAX_SIZE == head)
/* обработка ошибки - переполнение очереди */
a[tail] = value;
tail = (tail + 1) % MAX_SIZE;
}
Извлечение элемента
Удаление элемента требует только циклического увеличения индекса head. Должна быть предусмотрена проверка на удаление из пустой очереди.
int pop() {
if (head == tail)
/* обработка ошибки - нет элементов для извлечения */
int tmp = head;
head = (head + 1) % MAX_SIZE;
return a[tmp];
}
Ниже приведён полный код реализации очереди на массиве. Переполнение и попытка извлечения из пустой очереди выявляются с помощью конструкции assert (заголовочный файл <assert.h> либо <cassert>).
class Queue {
static const int MAX_SIZE = 100;
int a[MAX_SIZE];
int head, tail;
public:
Queue() {
head = tail = 0;
}
void enqueue(int value) {
assert((tail + 1) % MAX_SIZE != head);
a[tail] = value;
tail = (tail + 1) % MAX_SIZE;
}
int dequeue() {
assert(head != tail);
int tmp = head;
head = (head + 1) % MAX_SIZE;
return a[tmp];
}
bool isEmpty() {
return head == tail;
}
};
Очередь в STL
В стандартной библиотеке шаблонов C++ присутствует шаблон queue<T>. Для возможности его использования требуется подключить заголовочный файл <queue> и пространство имён std:
#include <iostream>
#include <queue>
using namespace std;
int main() {
queue<int> q;
for (int i = 1; i < 6; i++)
q.push(i);
while (!s.empty()) {
cout << q.front() << ' ';
q.pop();
}
return 0; //результат "1 2 3 4 5 "
}
STL предоставляет следующий набор методов для очереди:
| queue<T>() | — конструктор; | ||
| void | push(const T& x) | — добавление элемента; | |
| void | pop() | — удаление элемента. Обратите внимание на то, что значение удаляемого элемента не возвращается; | |
| T& | front() | — получение значения элемента в голове очереди. Этот метод не производит удаление элемента; | |
| T& | back() | — получение значения элемента в хвосте очереди. Этот метод не производит удаление элемента; | |
| bool | empty() | — проверка на пустоту; | |
| size_t | size() | — получение количества элементов в очереди. Метод возвращает беззнаковое целое число. |
Дек
Дек (англ. deque, double-ended queue) — тип, представляющий двустороннюю очередь, оба конца которой могут принимать и возвращать элементы. Интерфейс дека похож на интерфейс очереди, но содержит по паре методов вставки и удаления (для начала и конца двусторонней очереди). Дек естественным образом реализуется на двусвязном списке или на массиве.
В стандартной библиотеке шаблонов C++ шаблон std::deque<T>, объявленный в заголовочном файле <deque>, является базой для шаблонов стека и очереди и поддерживает значительно более широкий набор операций по сравнению с ними (в том числе доступ к элементам с помощью метода at() или оператора [], вставки значения в любую позицию с помощью метода insert(), доступ к итераторам и т. д.). Вставка элементов в дек STL производится с помощью методов push_front() и push_back(), удаление — с помощью pop_front() и pop_back().
Ссылки
Теория:
- e-maxx.ru — Модификация очереди для нахождения минимума
- neerc.ifmo.ru/wiki — Очередь
- brestprog.by — Простейшие структуры данных: стек, очередь, дек
- algorithmica.org — Стек и другие структуры данных
- opendatastructures.org — ArrayQueue
- opendatastructures.org — Queue operations via SLList
- algs4.cs.princeton.edu/lectures — 1.3 Stacks and Queues
Демонстрация:
- visualgo.net — Queue
- www.cs.usfca.edu — Queue: Array Implementation
- www.cs.usfca.edu — Queue: Linked List Implementation
Код:
- indy256/codelibrary/cpp/structures/queue_min.cpp
- ADJA/algos/DataStructures/QueueWithMinimum.cpp
- kevin-wayne/algs4/Queue.java
- kevin-wayne/algs4/LinkedQueue.java
- kevin-wayne/algs4/ResizingArrayQueue.java
Задачи: